Continuons donc avec les connaissances et savoir-faire exigibles pour l’épreuve de physique du bac. Je sais que mes lecteurs qui ne passent pas le bac n’apprécient que moyennement ces articles un peu trop technique… un peu de patience, dans 15 jours c’est fini et on pourra à nouveau penser à d’autres choses…

Après l’exposé des lois de Newton vient l’application à quelques cas suffisamment simple pour permettre une résolution complète du mouvement : chute verticale d’un solide (avec ou sans frottement), mouvements plans (mouvements paraboliques et satellites) et système oscillant.

Commençons par la chute verticale d’un solide.

Attention dans cet article (comme tous ceux de la mécanique), les vecteurs sont notés en gras :
ainsi g = g.u_z est équivalent à

Définir un champ de pesanteur uniforme.

Le champ de pesanteur est un champ vectoriel. C’est à dire qu’en tout point de l’espace, on peut y définir le vecteur pesanteur. Un champ uniforme est un champ qui a la même valeur en tout point de l’espace.

Un champ de pesanteur uniforme est donc un ensemble de vecteur dont la direction, le sens et la valeur sont les mêmes en tout point de l’espace.

Connaître les caractéristiques de la poussée d’Archimède.

La poussée d’Archimède est une force qui s’exerce sur tout corps immergé dans un fluide (liquide ou gaz). Elle est donc définies par une direction, un sens et une valeur. En l’occurence :

• Direction : verticale
• sens : vers le haut
• valeur : égale au poids du fluide déplacé

Ainsi pour un objet de volume V₀ complètement immergé, ce poids est égal à ?_fV₀g où ?_f est la masse volumique du fluide.

Chute verticale avec frottement

Appliquer la deuxième loi de Newton à un corps en chute verticale dans un fluide et établir l’équation différentielle du mouvement, la force de frottement étant donnée.

Ah, enfin, c’est là que les choses sérieuses peuvent commencer.

Imaginons donc un corps, lâché à l’instant t=0 de sorte à ce que son centre d’inertie soit au point O à cet instant. On se munira d’un repère Oxyz tel que z soit dirigé positif vers le bas. Bien entendu le référentiel est galiléen sinon on ne pourra pas appliquer la 2ème loi de Newton.

Ce corps est soumis au poids (P=mg),à la poussée d’Archimède (P_a=-?_fV₀g) et à une force de frottement (f qui est opposée au mouvement, soit proportionnelle à v, soit proportionnelle à v² selon l’énoncé).

La seconde loi de Newton s’écrit : ? f_ext=m a_G soit P + P_a + f = m a_G

Comme toutes les forces sont verticales, on peut projeter sur l’axe vertical et écrire mg – ?_fV₀g – f=m a_G

a_G l’accélération est égale à la dérivée de v (vitesse verticale) que l’on note généralement dv/dt et f est soit égale à k.v soit égale à k.v². On obtient donc :

mg – ?_fV₀g – k.v = m dv/dt
ou
mg – ?_fV₀g – k.v²=m dv/dt
selon l’expression de la force de frottement.

Et voilà pour l’équation différentielle du mouvement.

Connaître le principe de la méthode d’Euler pour la résolution approchée d’une équation différentielle.

Lors des révisions avec mes élèves, il semble que ce point n’est pas laissé un souvenir impérissable…
Supposons que nous ayons une équation différentielle de la forme a + b.v = v'(t).

L’approximation d’Euler consiste à écrire que

v(t+?t) = v(t) + v'(t). ?t

Ainsi, si l’on connait v(0), on peut écrire (en appliquant l’équation différentielle) que v'(0) = a + b.v(0).
On peut donc calculer la valeur de v à l’instant ?t en utilisant l’approximation d’Euler :

v(?t) = v(0) + v'(0). ?t

Ce qui nous permet de calculer v'(?t) = a + b.v(?t) d’où l’on peut déduire v(2?t) par Euler d’où l’on déduit v'(2?t) par l’équation différentielle, d’où l’on déduit .v(3?t).. etc. c’est une méthode itérative; c’est à dire que par une succession de petit calcul on peut finir par connaître v à chaque pas ?t.

Chute verticale libre

Définir une chute libre, établir son équation différentielle et la résoudre.

Une chute libre est une chute dans laquelle le système considéré n’est soumis qu’à son poids.

Dans l’étude d’un tel mouvement, on prendra encore une fois un axe vertical dirigé vers le bas. Le poids s’exprime donc P = mg avec g = g.u_z

On considérera un mouvement vertical, c’est à dire que la vitesse initiale est verticale.

Ainsi, si on applique la seconde loi de Newton, on n’aura simplement P = ma qui se réduit à a = g ce qui est la plus simple expression de la 2de loi de Newton que l’on puisse avoir sur Terre.

On considère un mouvement vertical : le vecteur accélération est donc simplement a = dv/dt.u_z. Ainsi, l’équation différentielle du mouvement est

dv/dt = g
qui s’intègre en v(t) = g.t + A où A dépend des conditions initiales

Imaginons que v(0) soit non nul et égal à une valeur v₀. Si l’on prend l’expression v(t) = g.t + A à t=0, on trouve A=v₀ et

v(t) = g.t + v₀

D’autre part, v = dz/dt on en déduit donc

dz/dt = g.t + v₀
qui s’intègre en z(t) = ½ . g.t² + v₀.t + B
où B est une constante d’intégration

Déterminer B est un jeu d’enfant, il suffit de considérer les conditions initiales :

z(0) = z₀ et z(t) = ½ . g.t² + v₀.t + z₀

Voilà qui est fait pour la chute libre verticale !

Définir un mouvement rectiligne uniformément accéléré.

Trop facile. Un mouvement rectiligne uniformément accéléré est un mouvement dont la trajectoire est une droite et dont l’accélération est constante, indépendante du temps.

Ex de mouvement rectiligne uniforme : la chute libre ! Voir ci-dessus.

Savoir exploiter des reproductions d’écrans d’ordinateur (lors de l’utilisation d’un tableur grapheur) correspondant à des enregistrements expérimentaux.

Savoir exploiter des courbes v =f(t) pour : reconnaître le régime initial et/ou le régime asymptotique, évaluer le temps caractéristique correspondant au passage d’un régime à l’autre, déterminer la vitesse limite

Pour ces deux points, puisqu’un schéma vaut mieux qu’un discours :

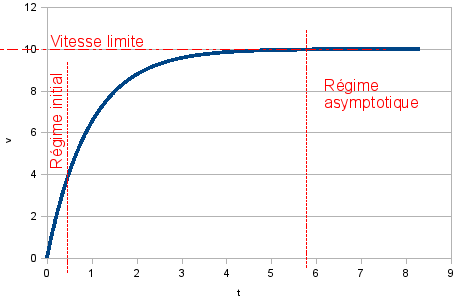
Sur le schéma ci-dessus, la vitesse limite est de 10 m/s et il faut 5 seconde pour passer du régime initial (mouvement rectiligne uniformément accéléré) au régime asymptotique (mouvement rectiligne uniforme)

Dans le cas de la résolution par méthode itérative de l’équation différentielle, discuter de la pertinence des courbes obtenues par rapport aux résultats expérimentaux (choix du pas de résolution, modèle proposé pour la force de frottement)

Il s’agit simplement d’être capable de faire le lien entre un graphique expérimental et un modèle.

Le pas de résolution est le ?t dont il a été question dans la méthode d’Euler. Dans l’idéal il faudrait qu’il soit tout petit pour que l’approximation d’Euler fonctionne. Le graphique ci-dessous montre 1 courbe obtenue par la méthode d’Euler (rouge) et une acquisition expérimentale (bleue) :

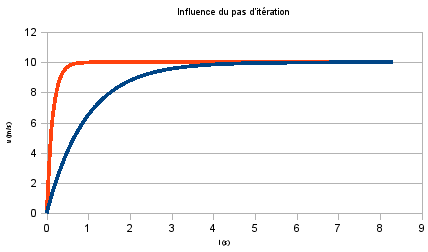
La courbe rouge a été calculée avec un pas trop grand et la vitesse atteint trop vite sa valeur limite. En diminuant le pas d’itération, on peut obtenir la courbe bleue par Euler.

Pour ce qui est de l’influence des forces de frottements, le graphique ci-dessous montre une modélisation en supposant une force de frottement en v² (courbe en rouge) :

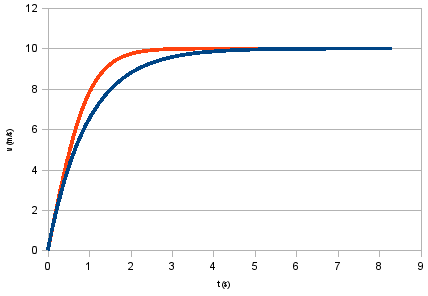
Clairement, ce modèle ne convient pas et on testera le modèle « force de frottement proportionnelle à v » pour voir s’il colle à la courbe expérimentale.