Continuons avec les connaissances et savoir-faire exigibles pour l’épreuve de physique du bac avec ce qu’il faut retenir du dipôle RLC. Comme d’habitude, les connaissances et savoir-faire exigibles du programme sont en gras :

Lorsqu’on branche un condensateur chargé à une bobine, celui-ci tend à vouloir se décharger (voir le cas du dipôle RC). Des charges ont donc tendance à se déplacer dans le circuit. Mais une bobine « n’aime » pas que le courant qui le traverse varie (voir l’étude du dipôle RL). Elle va donc avoir tendance à ralentir cette décharge. Cependant, progressivement, le condensateur arrive à imposer un courant et il va progressivement se décharger. Lorsque la charge qu’il porte est nulle, le transfert de charge pourrait s’arrêter là mais comme la bobine impose une continuité du courant, elle va obliger le condensateur à se charger dans l’autre sens et ainsi de suite : on observe des oscillations de la tention aux bornes du condensateur.

Définir et reconnaître les régimes périodique, pseudo-périodique et apériodique.
Savoir tracer l’allure de la tension aux bornes du condensateur en fonction du temps pour les régimes périodique, pseudo-périodique et apériodique.

Pour le processus qui vient d’être décrit, 3 régimes sont possibles selon la valeur de la résistance totale du circuit. Dans le cas où la résistance est nulle, on observe un régime périodique :

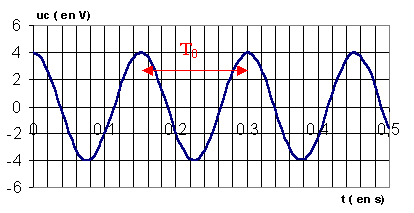
source : http://montblancsciences.free.fr

Dans le cas où la résistance du circuit est faible, on observe un régime pseudo-périodique :

source : http://montblancsciences.free.fr

Dans le cas d’une grande résistance, on observe un régime apériodique :

source : http://montblancsciences.free.fr

Dans le cas d’un amortissement négligeable, effectuer la résolution analytique pour la tension aux bornes du condensateur ou la charge de celui-ci.
En déduire l’expression de l’intensité dans le circuit.

Envisageons un circuit constitué d’un condensateur de capacité C et une bobine idéale d’inductance L. A t=0, le condensateur est chargé, portant une tension U₀. La résolution analytique s’effectue toujours selon la même méthodologie :

1. Obtention de l’équation différentielle – condensateur et bobine sont en série et vérifient donc u_C+u_L=0. Pour obtenir l’équation vérifiée par u_C, il faut exprimer u_L en fonction de u_C. On sait que u_L=L.di/dt d’une part et que i=dq/dt donc on peut en déduire que u_L=Ld²q/dt² où d²q/dt² est la dérivée seconde par rapport au temps de la charge (la dérivée de la dérivée : q »(t) en notation mathématique). Or q=C.u_C dont u_L=LCd²uC/dt et u_C vérifie :
   u_C+LC.d²u_C/dt²=0.
2. Résolution de l’équation différentielle – cette équation admet des solutions de la forme : u_C(t)=U_m.cos(2?.t/T₀+?₀) où U_m représente l’amplitude (en Volt), T₀ , la période (en s) et ?₀, la phase à l’origine (en rad). La détermination de ces grandeurs se fait en 2 étapes : en injectant cette expression dans l’équation différentielle puis en appliquant les conditions initiales. La dérivée de u_C(t) par rapport au temps est
   du_C/dt= -2?/T_0.U_m.sin(2?.t/T₀+?₀).
   La dérivée seconde est donc d²u_C/dt²= -(2?/T_0)².U_m.cos(2?.t/T₀+?₀). Si l’on injecte cette dernière expression dans l’équation différentielle ainsi que celle de u_C(t), on obtient :
   U_m.cos(2?.t/T₀+?₀₎ -LC(2?/T_0)².U_m.cos(2?.t/T₀+?₀)=0
   ce qui est équivalent à :
   (1-LC(2?/T₀)²)U_m.cos(2?.t/T₀+?₀₎ =0 qui n’est possible pour tout t que si T₀=2?.?(LC)
3. Obtention de i(t) – De l’expression de u_C(t), on peut déduire i qui est égale à dq/dt donc à C.du_C/dt ? i(t)=-2?/T_0.C.U_m.sin(2?.t/T₀+?₀)
4. Conditions initiales – Les conditions initiales sont uC(t=0)=U₀ et i(t=0)=0. Si l’on applique les expressions trouvées précédemment, on obtient :
   U_m.cos(?₀)=U₀ et U_m.sin(?₀)=0 qui implique que ?₀=0 et U_m=U₀.

Pour finir, nous avons donc les expressions suivantes :

u_C(t)=U₀.cos(2?.t/T₀) où T₀=2?.?(LC)
q(t)=C.u_C(t)=Q₀.cos(2?.t/T₀) où Q₀=C.U_{0
i(t)=dq/dt=}-I_m.sin(2?.t/T₀) où I_m=2?.Q₀/T₀

Connaître l’expression de la période propre, la signification de chacun des termes et leur unité.

De la résolution analytique, on a déduit T₀=2?.?(LC) où L est l’inductance de la bobine et C, la capacité du condensateur.

On peut vérifier que cette expression est homogène :

• de l’étude du dipôle RC, on avait déduit que RC est homogène à un temps,
• de l’étude du dipôle RL, on avait déduit que L/R est homogène à un temps,
• on en déduit que LC est homogène à L/R.RC=Temps²
• donc ?(LC) est homogène à un temps.

Savoir que le dispositif qui entretient les oscillations fournit l’énergie évacuée par transfert thermique.
Savoir interpréter en terme d’énergie les régimes périodique, pseudo-périodique, apériodique et entretenu.

Les oscillations observées dans le cas où l’amortissement est nul (pas de résistance), correspondent en fait à un échange d’énergie entre le condensateur et la bobine : le condensateur a initialement emmagasiné une énergie sous forme électrique (1/2.C.u_C²) qu’il transmet à la bobine (1/2.L.i²).

A chaque transfert,  la résistance dissipe de l’énergie puisqu’elle est traversée par un courant électrique (une résistance dissipe une énergie R.i² à chaque instant). Ainsi, l’énergie totale du circuit électrique diminue progressivement à chaque transfert d’énergie entre le condensateur et la bobine et les oscillations s’amortissent.

Dans le cas où la résistance est très élevée, toute l’énergie est dissipée dès le premier transfert et la partie de ping-pong avec l’énergie entre condensateur et bobine ne se fait pas.

Pour entretenir les oscillations, il est nécessaire de « réinjecter » de l’énergie à chaque transfert, ce qui se fait à l’aide d’un dispositif qui fournit l’énergie dissipée  par la résistanc.

Savoir exploiter un document expérimental pour:

• identifier les tensions observées,
• reconnaître un régime
• montrer l’influence de R et de L ou C sur le phénomène d’oscillations
• déterminer une pseudo-période.

La tension aux bornes du condensateur est initialement égale à U₀. Aux bornes de la résistance, elle est nulle initialement puisqu’il n’y a pas de courant.

L’influence de R, L et C a été discutée dans les points précédents.

La pseudo-période se détermine en prenant 2 passages par zéro dans le même sens de la tension aux bornes du condensateur. Cette pseudo-période est voisine de la période propre calculée précédemment (T₀=2?.?(LC)).

Sur le site de l’académie de Caen, on trouve une petite application qui simule la tension aux bornes d’un condensateur.