I – Quelques mots de vocabulaire :
Définitions :
On appelle expérience aléatoire une expérience dont le résultat final est seulement dû au hasard.
Chaque résultat possible d’une expérience aléatoire est une issue de l’expérience.
On note l’ensemble des issues s’appelle l’univers et se note avec la lettre grecque oméga : ?.
Remarque : Evidemment, l’expérience a plusieurs issues (sinon il n’y a plus de hasard !) et il est impossible de prédire de façon certaine le résultat final avant la fin de l’expérience.
Exemple : le lancer d’un dé (équilibré) à 6 faces
a) Est-ce une expérience aléatoire ? Oui, le lancer d’un dé est une expérience aléatoire. Il est impossible de prédire le résultat final.
b) Quelles sont les issues de l’expérience ? Les issues relatives au lancer d’un dé à 6 faces sont les 6 faces du dé, c’est-à-dire : la face 1, la face 2, la face 3, la face 4, la face 5, la face 6.
c) On note ? = { 1 ; 2 ; 3 ; 4 ; 5 ; 6 }.
Définitions :
Un événement est une condition (phrase), qui selon l’issue de l’expérience est réalisée ou n’est pas réalisée.
Un événement élémentaire est un événement qui ne peut être réalisé que par une seule issue.
Exemples avec l’expérience du lancer de dé à 6 faces :
L’événement « Obtenir un nombre pair » est réalisé par : 3 issues (la face 2, la face 4 et la face 6).
L’événement « Obtenir le nombre 5 » est réalisé par : 1 seule issue (la face 5).
Citer un événement élémentaire : « Obtenir le nombre 5 », ou « Obtenir le nombre 1 » ou « Obtenir le nombre 4 », ou « Obtenir un nombre premier pair » qui est identique à « Obtenir le nombre 2 », ou …
Exercice : [WpProQuiz 3]
* * * * * * * * * * * * * * * * * * * *
Dans ce chapitre, nous nous intéressons à des probabilités elles sont reliées à la définition des fréquences. Qu’est-ce qu’une fréquence ?
Définition : Une fréquence est le quotient du nombre de répétitions de ce qui nous intéresse par le nombre total d’éléments de notre référence.
Exemples :
a) Dans la phrase extraite du livre Les revenentes de Georges Perec :
« En ce mement, certes, t’es le chef, mets – beleve me – ce temps est bref et je préfère être dens mes semelles qe dens tes empègnes ! »
Quelle est la fréquence d’apparition de la lettre « e » dans la phrase entière ? 36 / 98.
Quelle est la fréquence d’apparition de la lettre « e » dans le mot « bref » ? 1 / 4
b) Portez ce vieux whisky au juge blond qui fume.
Un pangramme est une phrase qui contient toutes les lettres de l’alphabet.
Quelle est la fréquence d’apparition de la lettre « o » dans ce pangramme ? 2 / 37
Rappelons aussi la définition d’une proportion.
Définition : Une proportion est le quotient d’un nombre d’éléments (qui nous intéressent) par le nombre total d’éléments.
Exemple : Dans une classe, il y a 12 filles et 14 garçons.
Quelle est la proportion de filles dans la classe ? Il y a en tout 26 élèves.
La proportion de filles est donc : 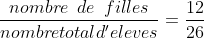
II – Simulation du lancer d’un dé à 6 faces (TP – Tableur)
Définition : Lorsque l’on répète un très grand nombre de fois une expérience aléatoire, la fréquence à laquelle se réalise un événement se rapproche d’une « fréquence théorique » appelée probabilité de cet événement.
TP Dé à 6 faces
III – Probabilité d’un événement
Définition : Lorsque l’on effectue un très grand nombre de fois une expérience aléatoire, la fréquence à laquelle se réalise un événement se rapproche d’ « une fréquence théorique » appelée la probabilité de l’événement.
Définitions :
Un événement dont la probabilité est nulle est l’événement impossible.
Un événement dont la probabilité est 1 est l’événement certain.
Propriétés :
a) La probabilité est un nombre compris entre 0 et 1.
b) La somme des probabilités d’obtenir chaque issue est égale à 1.
Définition et propriété : Cas de l’équiprobabilité
Pour une expérience aléatoire, lorsque tous les événements élémentaires ont la même probabilité : on parle de situation d’équiprobabilité.
Dans ce cas, la probabilité d’un événement est égale au nombre d’issues qui réalise l’événement sur le nombre total d’issues.
Exemple : La probabilité de l’événement « obtenir un nombre pair » est : 3/6 = 1/2.
