Objectifs du chapitre :
– Comparer des angles sans leurs mesures.
– Savoir mesurer et construire des angles.
– Connaître la définition de la bissectrice.
Activité : comparaison d’angles
I – Vocabulaire et notation
Schéma d’un angle : le sommet de l’angle et les côtés de l’angle.
Un angle de mesure 0° est appelé angle nul.
Un angle entre 0° et 90° est appelé angle aigu.
Un angle de mesure 90° est appelé angle droit.
Un angle entre 90° et 180° est appelé angle obtus.
Un angle de mesure 180° est appelé angle plat
Un angle se note souvent par trois lettres recouvertes d’un accent circonflexe. La lettre au milieu est le point situé au sommet de l’angle.
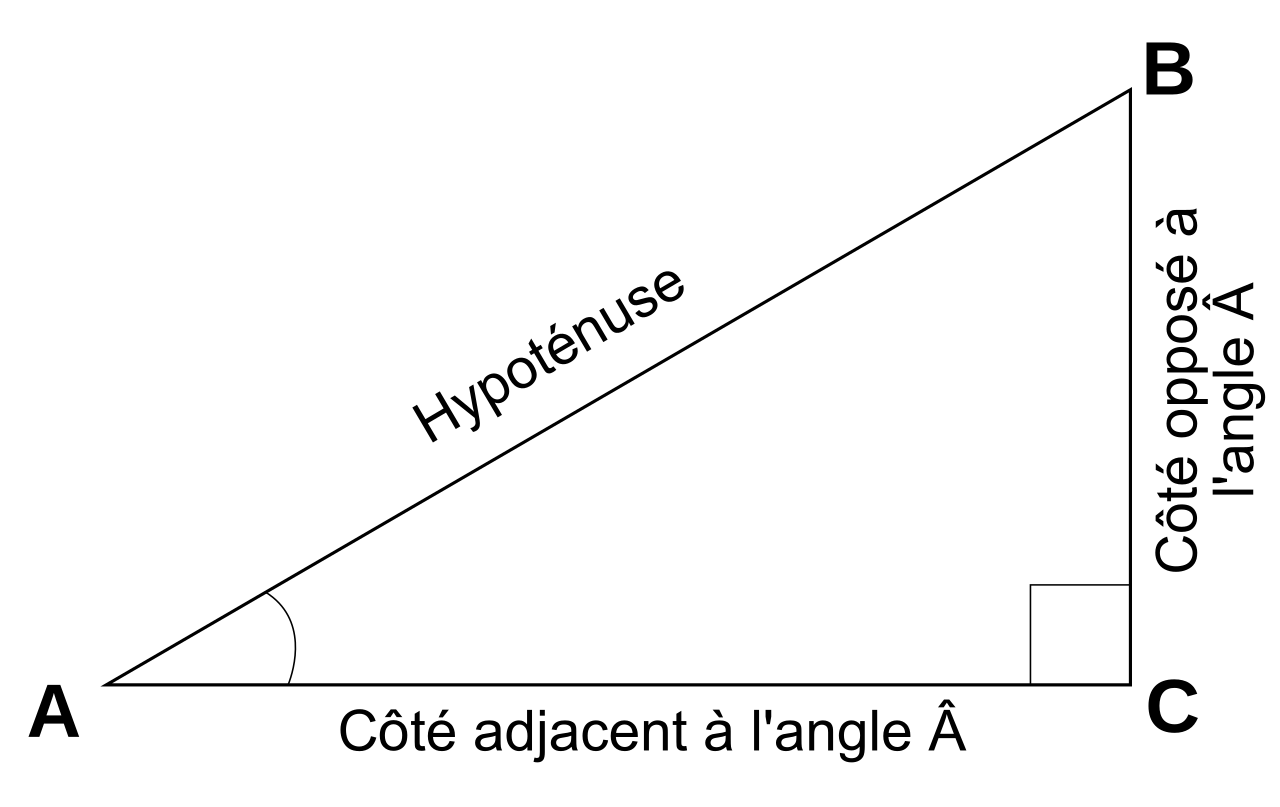
II – Construire un angle et utilisation du rapporteur
Exercice interactif
III – La bissectrice
Définition : La bissectrice d’un angle est la droite qui partage cet angle en deux angles égaux.
Construction au compas

IV – Angles d’un triangle
Activité : Construire un triangle quelconque, puis colorier les angles.
Découper le triangle puis couper le triangle au milieu de chacun de ses côtés.
Coller les angles ensemble (les 3 pointes seront réunies ensemble).
Propriétés :
La somme des mesures des angles d’un triangle est égale à 180°.
Dans un triangle rectangle, la somme des mesures des angles aigus est égal à 90°.
Exercices :
Calculer les mesures des angles d’un triangle équilatéral.
Calculer les mesures des angles d’un triangle rectangle isocèle.