En géométrie spatiale (3D), certains solides sont rois : ce sont les solides de Platon. Ils sont au nombre de cinq. Nous allons apprendre à les connaitre mais aussi essayer de comprendre pourquoi ils ne sont que cinq et ce qui fait qu’ils soient mis à part. Il te faudra connaître un peu le vocabulaire sur la géométrie spatiale (sommet, arête, face, polyèdre, …) mais aussi avoir quelques connaissances sur les angles.
Avant de commencer, il me semble important de vous les présenter. Voici donc les cinq solides de Platon avec leur joli nom :
[su_table alternate= »no » class= »div.hotbox {-moz-border-radius:20px} »]
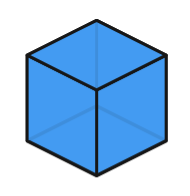
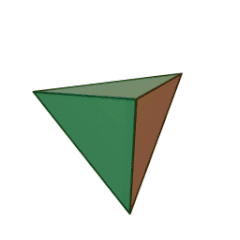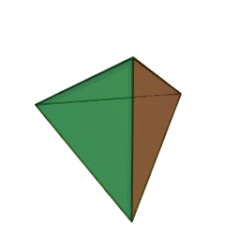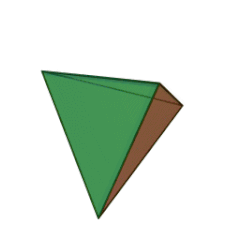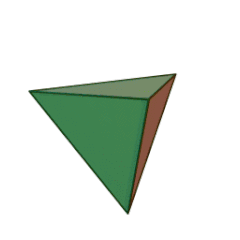
| Tétraèdre | Héxaèdre (Cube) | Octéaèdre | Dodécaèdre | Icosaèdre |
 |
 |
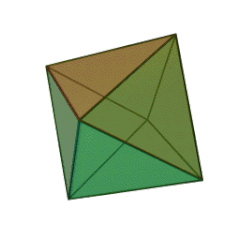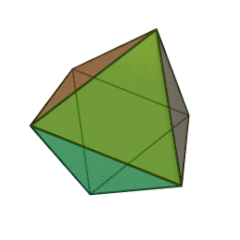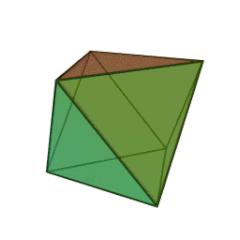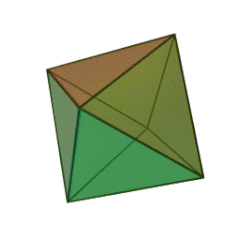 |
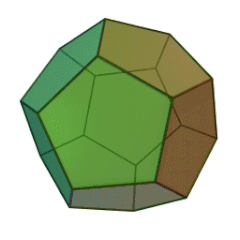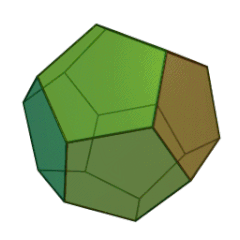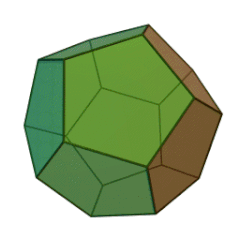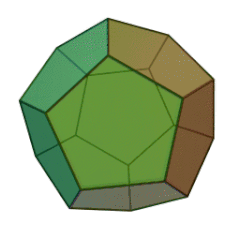 |
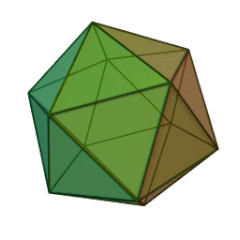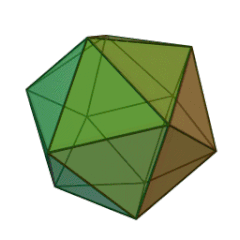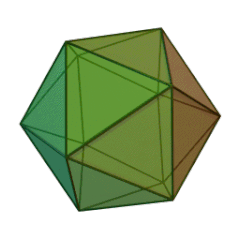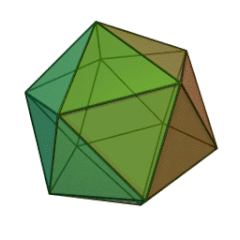 |
[/su_table]
[su_note note_color= »#00A1B5″ text_color= »#ffffff » radius= »8″]Pour information, le vrai nom du cube est HEXAEDRE.[/su_note]
Comme pour tout solide de l’espace. Nous pouvons créer une carte d’identité en comptant le nombre de sommets, de faces, d’arêtes :
[su_table alternate= »no » class= »div.hotbox {-moz-border-radius:20px} »]
| Solide | Tétraèdre
|
Héxaèdre (Cube)
|
Octaèdre
|
Dodécaèdre
|
Icosaèdre
|
| Nombre de sommets | 4 | 8 | 8 | 20 | 12 |
| Nombre d’arêtes | 6 | 12 | 12 | 30 | 30 |
| Nombre de faces et leur nature | 4 triangles équilatéraux | 6 carrés | 8 triangles équilatéraux | 12 pentagones réguliers | 20 triangles équilatéraux |
[/su_table]
Alors qu’ont-ils de particuliers ?
Pour commencer, ce sont des polyèdres convexes. C’est à dire que le chemin LE PLUS COURT pour joindre deux sommets du solide passe NECESSAIREMENT à « l’intérieur » du solide. Voici l’exemple de deux solides : l’un non convexe et l’autre qui l’est :
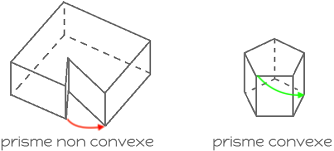
[su_note note_color= »#00A1B5″ text_color= »#ffffff » radius= »8″]Pour la culture générale, sache que lorsqu’un solide n’est pas CONVEXE, on dit qu’il est CONCAVE. [/su_note]
De plus, chaque solide est composé du même polygone régulier égaux :
- Des triangles équilatéraux pour le Tétraèdre, l’Octaèdre, et l’Icosaèdre ;
- Des carrés pour le Cube ;
- Des pentagones réguliers pour le Dodécaèdre.
Ce n’est pas toujours le cas. En effet de nombreux solides possèdent des faces de formes diverses comme sur cet exemple qui possède des faces triangulaires et des faces rectangulaires :
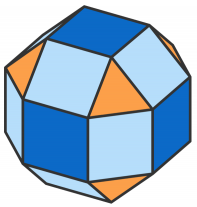
Et enfin une autre particularité, qui peut paraître anodine mais qui aura son importance pour après ; le même nombre de faces se rencontre en un même sommet :
- Trois triangles équilatéraux se rencontrent pour former un sommet dans le Tétraèdre ;
- Trois carrés se rencontrent pour former un sommet du Cube ;
- Quatre triangles équilatéraux se rencontrent pour former un sommet de l’Octaèdre ;
- Trois pentagones réguliers se rencontrent pour former un sommet du Dodécaèdre ;
- Cinq triangles équilatéraux se rencontrent pour former un sommet de l’Icosaèdre.
[su_note note_color= »#f3b041″ text_color= »#ffffff » radius= »8″]
Pour conclure, Un solide est dit de Platon si et seulement si :
- il est convexe
- formé de faces régulières et identiques
- que le même nombre de faces se rencontre en un sommet
[/su_note]
Maintenant que nous avons vu la définition du Solide de Platon. Essayons de comprendre pourquoi il n’y en a que cinq ; ni plus ni moins. Pour cela nous allons partir de la dernière particularité : « Le même nombre de faces se rencontre en un sommet ».
Comme les faces doivent être obligatoirement des polygones réguliers, nous pouvons lister les premiers d’entre eux :
- le triangle équilatéral (3 côtés)
- le carré (4 côtés)
- le pentagone régulier (5 côtés)
- l’hexagone régulier (6 côtés)
- l’heptagone régulier (7 côtés)
- …
Et commençons avec le premier le triangle équilatéral. Combien de triangle équilatéral pouvons-nous regrouper afin de former un sommet ?
Nous avons regroupé des triangles équilatéraux identiques :
[h5p id= »51″]
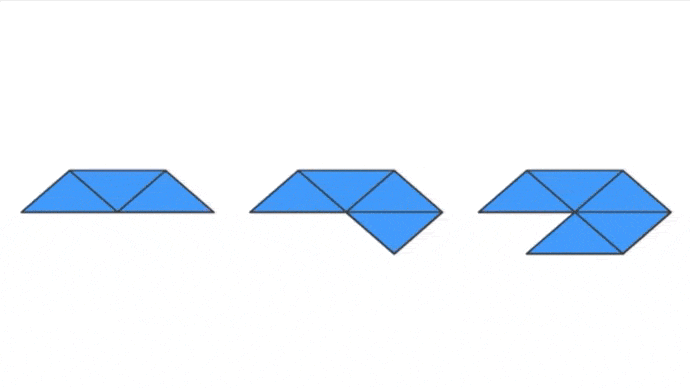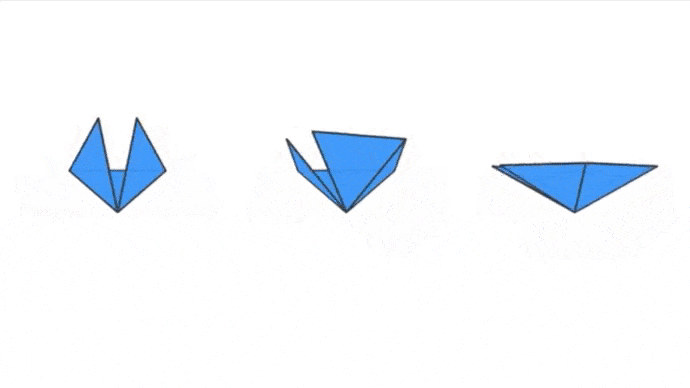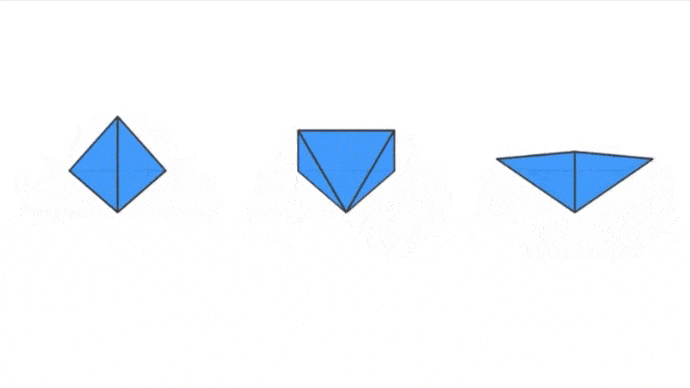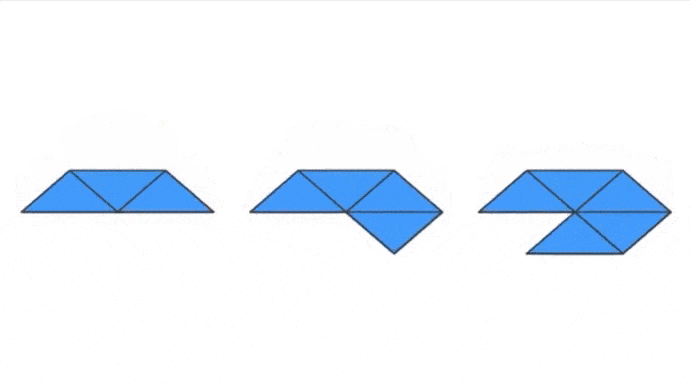
Alors ? Trouvé ? Voici deux petites animations afin de te faire comprendre ce qui fonctionne pour certains et ce qui ne fonctionne pas pour d’autres :
[su_row class= » »]
[su_column size= »1/2″ center= »no » class= » »]
[/su_column]
[su_column size= »1/2″ center= »no » class= » »]
[/su_column]
[/su_row]
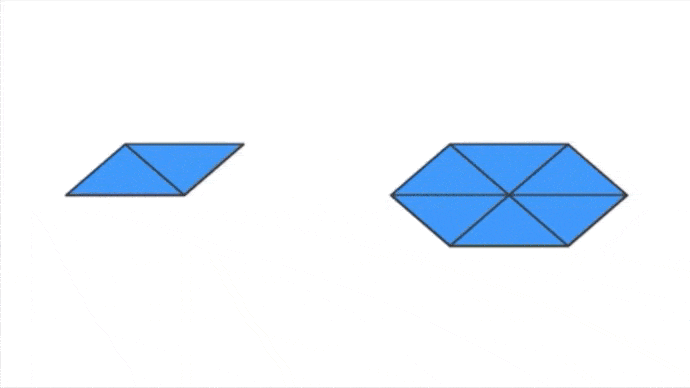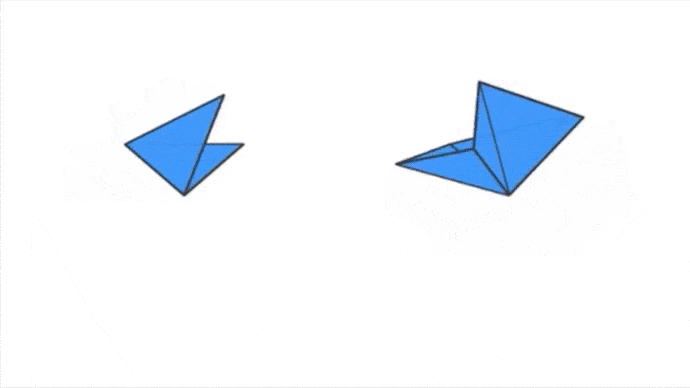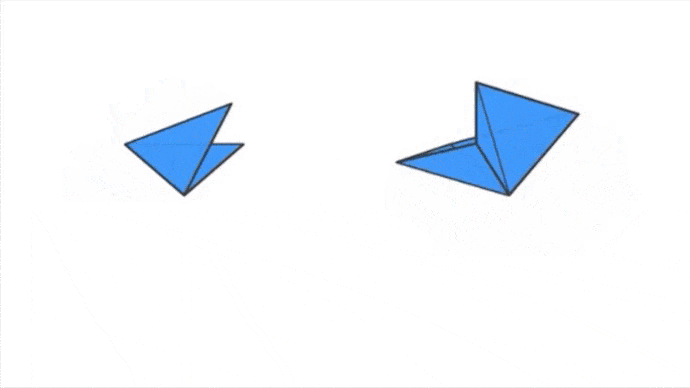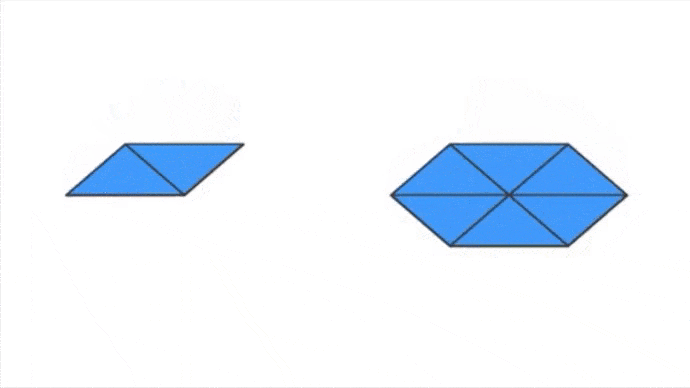
Pour les deux configurations de droite, on a un problème. Pour le cas de deux triangles équilatéraux, il n’y en a pas assez afin de former un sommet. Les deux triangles vont finir par se superposer et ne former qu’une figure plane. Pour le cas de six triangles équilatéraux, la configuration pose déjà problème au départ, elle forme une figure plane, si on essaye de la déformer afin de lui donner du « volume », elle finira par former un début de solide mais qui ne sera pas convexe !
Par contre, les trois configurations de gauche fonctionnent.
- Dans le premier cas, trois triangles équilatéraux vont venir former un sommet, on a le début de notre Tétraèdre.
- Dans le second cas, quatre triangle équilatéraux vont venir former un sommet, on a le début de notre Octaèdre.
- Dans le troisième cas, cinq triangles équilatéraux vont venir former un sommet, on a le début de notre Icosaèdre.
[su_note note_color= »#41b4f3″ text_color= »#ffffff » radius= »8″]Il est assez évident que pour plus de six triangles équilatéraux, cela ne sera pas possible, les triangles finissant par se chevaucher.[/su_note]
Passons maintenant au carré. Combien de carrés pouvons-nous regrouper afin de former un sommet ?
Nous avons regroupé des carrés identiques :
[h5p id= »52″]
Alors ? Trouvé ? De la même manière que pour les triangles équilatéraux, nous pouvons imaginer ce qui va se passer :
- dans le cas de deux carrés, les plier va finir par les superposer et ne former qu’une figure plane et non un sommet d’un solide en 3D. Donc cela ne fonctionne pas.
- dans le cas de trois carrés, les plier va bien finir par former un sommet d’un futur solide convexe. Ici, nous avons le début d’un Cube.
- dans le cas de quatre carrés, nous avons déjà une figure plane, et la plier ne sera pas possible.
Maintenant passons, aux polygones réguliers de plus de 4 côtés, mais plutôt que de les faire un par un ; prenons les tous en même temps. 
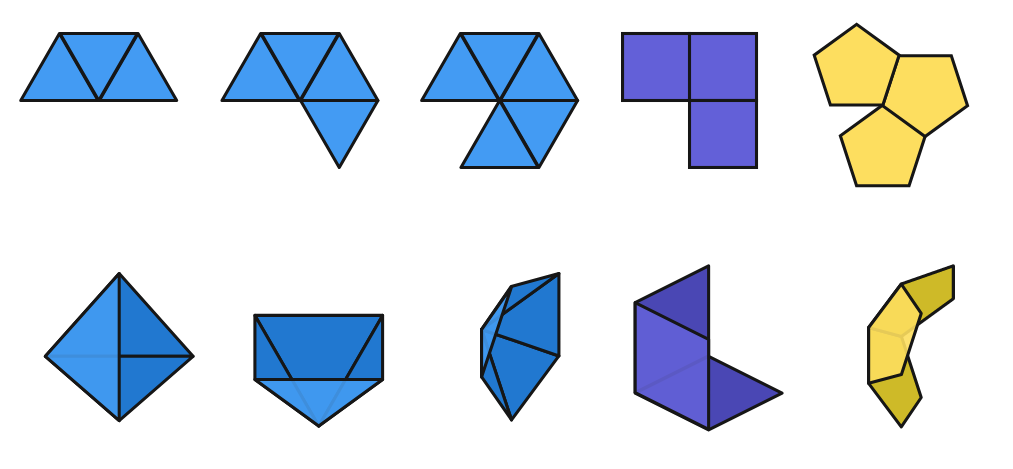
De la même manière qu’avant, nous pouvons les regrouper par paquet et essayer de voir si en les déformant nous pouvons obtenir un sommet. Nous pouvons déjà éliminer le regroupement de deux solides identiques nous avons vu que cela ne donnait jamais rien. Voici ce que cela donne pour les trois premiers solides dans des regroupements de trois faces :

- Pour le premier regroupement, cela fonctionnera bien. Nous avons le début du Dodécaèdre.
- Pour le deuxième regroupement, nous avons un problème. Les trois hexagones ferment entièrement l’angle du centre ; en effet 3×120°=360°. Il sera impossible de plier la figure.
- Pour le dernier regroupement, un autre problème intervient les angles des heptagones sont bien trop grand. Il est impossibles de les réunir par trois sans qu’il n’y ai une superposition.
- On peut raisonnablement comprendre que la conclusion sera la même pour l’octogone, les angles de celui-ci sont trop grand.
Nous avons donc relevé seulement cinq configurations qui fonctionnent :
Et voilà ! On obtient ainsi nos cinq solide de Platon :
[su_table alternate= »no » class= »div.hotbox {-moz-border-radius:20px} »]
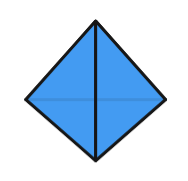
Tétraèdre |

Octaèdre |
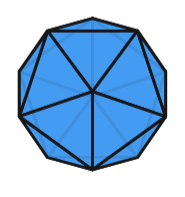
Icosaèdre |
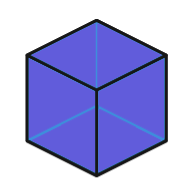
Cube |
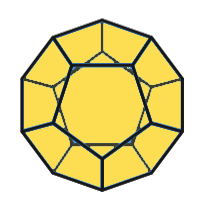
Dodécaèdre |
[/su_table]
Pour aller plus loin dans le sujet je t’invite à regarder cette vidéo :
[su_youtube_advanced url= »https://youtu.be/eDsFmYur9Yo » playlist= » » width= »100% » height= »100% » responsive= »yes » controls= »yes » autohide= »alt » autoplay= »no » mute= »no » loop= »no » rel= »yes » fs= »yes » modestbranding= »no » theme= »dark » wmode= » » playsinline= »no » title= » » class= » »]