Victor Vasarely, de son vrai nom Vásárhelyi Gy?z? (Pécs, 9 avril 1906 – Paris, 15 mars 1997), est le plasticien hongrois reconnu comme étant le père de l’art optique ou Op art. Ses œuvres sont autant d’occasions de faire de la géométrie au collège.

Niveau
Fin de cycle 3, sixième
Pré-requis
- Avoir déjà analysé une figure dans le but de comprendre comment elle peut être construite (nommer, coder, mesurer, etc)
- Avoir déjà manipulé un logiciel de géométrie dynamique (GeoGebra). Voir par exemple : Geogebra-en-6eme-premiere-utilisation
Objectifs / B.0
- Comprendre le passage du dessin à la figure ou, comme le dit explicitement le B.O, dans les compétences travaillées :
(…) passer progressivement de la perception au contrôle par les instruments pour amorcer des raisonnements s’appuyant uniquement sur des propriétés des figures et sur des relations entre objets ;
- Réaliser un programme de construction
- Établir un petit raisonnement (pour le motif 6, défi)
- Croiser les enseignements de Mathématiques et d’Arts Plastiques, comme le précise le B.O :
Les activités de reconnaissance et de construction de figures et d’objets géométriques peuvent s’appuyer sur des réalisations artistiques (peinture, sculpture, architecture, photographie, etc.).
Déroulement
- Commencer par présenter l’oeuvre (et l’artiste) à l’aide d’un vidéo-projecteur. Faire commenter cette oeuvre par la classe. Le but est de faire le lien avec la géométrie. Distribuer ensuite les énoncés. Préciser que les deux derniers motifs sont des défis. En effet, leur construction rigoureuse reste très difficile pour des élèves de sixième. Dire que nous allons devoir comprendre comment ont été construits ces motifs pour pouvoir, à notre tour, les reproduire.
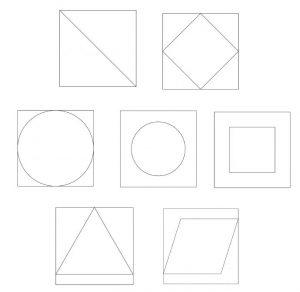
- Mettre ensuite les élèves en situation de recherche, ils devront, à l’aide de leurs instruments de géométrie, prendre des informations sur les dessins fournis. On veillera alors à ce que les points soient nommés, les dessins codés, des traits représentants des alignements tracés, etc.
Figures n°1 et 2 : les figures sont simples et à la portée de tous.
Figure n°3 : les élèves devront trouver comment obtenir le centre du cercle ainsi que son rayon. Le milieu du côté comme point de contact du cercle avec le carré fait partie du domaine de la figure géométrique construite. Certains élèves, restant dans le domaine de la perception, tenteront simplement de faire « toucher » le cercle. Cette question prendra tout son sens lors du passage à la géométrie dynamique, sous GeoGebra. On pourra alors zoomer sur un point « douteux » :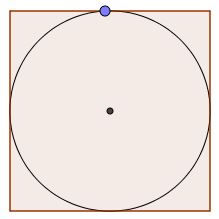
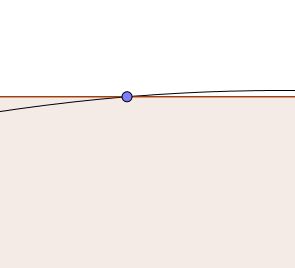
Figure n°4 : une analyse trop peu précise du dessin mènera certains élèves à prendre comme rayon le quart du côté du carré au lieu du quart de sa diagonale.
Figure n°5 : une construction approximative peut être acceptée.
Figure n°6 : certains élèves vont proposer la construction suivante basée sur des milieux :
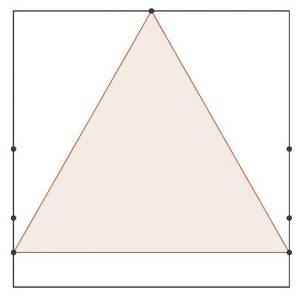
Il conviendra, dans un premier temps, de valider cette construction. On pourra néanmoins questionner les élèves sur la nature du triangle obtenu. Leur réponse est unanime, il est équilatéral. Cette affirmation sera mise en défaut sous GeoGebra mais dans un second temps.
Figure n°7 : Elle reste très difficile et peut n’être proposée qu’en « super défi » comme une façon de montrer aux élèves qu’il reste du chemin à parcourir et que, souvent, en mathématiques, certains problèmes restent partiellement résolus. - Dans un second temps, on pourra demander aux élèves de rédiger des programmes de construction correspondants à leurs analyses. On pourra distribuer des fiches à compléter qui pourront être bien pratique pour les scanner et projeter. Dans ce travail, une attention particulière sera portée sur le vocabulaire utilisé. On pourra alors distribuer un « lexique » des programmes de constructions.
Voici quelques productions d’élèves qui montrent, au travers du vocabulaire utilisé, le passage de la géométrie perceptive à la géométrie construite (cliquer pour agrandir) :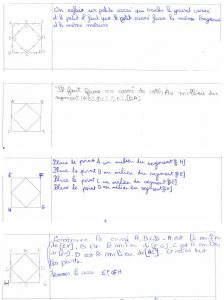

- Dans un troisième temps (ou indépendamment de la rédaction des programmes de construction, voire même en faisant des aller-retours entre les deux tâches), les élèves pourront réaliser leurs constructions sous GeoGebra. On pourra utiliser une version allégée du logiciel avec seulement les menus nécessaires.
Ce sera alors l’occasion de revenir sur le motif n°6 en utilisant l’outil Distance ou Longueur :
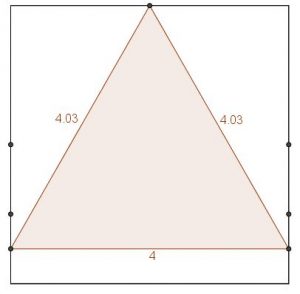
On relancera les élèves en leur demandant de comparer la mesure du côté du carré et celle du triangle à construire. - Pour finir, un bilan sur le motif n°6 permettra à tous d’avoir accès à une construction du triangle équilatéral. Une attention particulière sera lors portée davantage sur le vocabulaire que sur la recherche de la construction. En défi, on pourra proposer d’expliquer comment on peut être certain que le triangle obtenu est équilatéral. ce sera alors l’occasion de revenir sur la définition du cercle.
Prolongements
- On pourra demander aux élèves, ou à un groupe d’élèves, de se charger de réaliser l’oeuvre toute entière sous GeoGebra.
- Il existe d’autres œuvres susceptibles d’être travaillées dans le cours de mathématiques. Citons, par exemple Theo van Doesburg avec Arithmetic Composition, très intéressante pour construire des figures « à l’infini » :

Fichiers utiles
Énoncé_analyse.pdf
Énoncé_programme.pdf
Le_sixième_motif.pdf
Bilans_possibles.pdf
Affiche_Sikra_A3.pdf
références / liens
- A propos de l’analyse de figures géométriques et de la distinction entre dessin géométrique et figure géométrique, il faut citer l’excellent ouvrage de Jean-Philippe Rouquès et Hélène Staïner : « Des maths Ensemble et Pour Chacun – 6ème » édité par le CRDP des Pays de Loire.
- Le site de la fondation Vasarely à Aix-en Provence.
- L’IREM de Paris-Nord propose une série d’activités basée sur la tortue Logo (celle des 80’s) qui peuvent sans doute être adaptées au dessin sous Scratch.
- Le Petit vert n°132 de l’APMEP région Lorraine, page 37 à 45, propose un dossier Maths & Arts en classe de sixième assez complet.
Pour finir
La Hongrie, pays d’origine de Vasarely est liée à un bon nombre de célébrités. C’est la remarque que nous nous sommes faîtes mon épouse et moi même en visitant Budapest, il y a quelques jours. Citons, pour la photo, Robert Capa, pour la musique, Franz (Ferenc) Liszt et Béla Bartók, pour les mathématiques, Imre Lakatos et son formidable Preuves et Réfutations : essai sur la logique de la découverte mathématique, Paris, Éditions Hermann, 1984, et peut-être Ern? Rubik et son invention infernale des 80’s et puis puisqu’une exposition a lieu actuellement à Budapest sur cette artiste, Frida Kahlo par son père d’origine germano-austro-hongroise !






