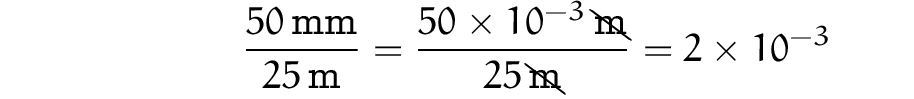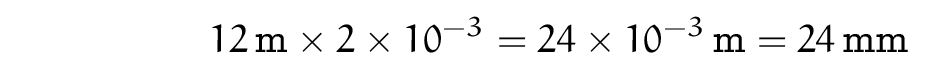Voilà une image à projeter en classe. C’est obligatoire, dès la sixième, tous les élèves doivent connaître ça !
Questionner les élèves sur cette oeuvre de Magritte, les laisser donner leur avis, s’exprimer et dire à ce qui connaissent déjà, de ne rien dévoiler.
Une pipe, on doit pouvoir y mettre du tabac dedans, l’allumer et la fumer. Ici, avec l’image projetée au tableau, impossible de bourrer la pipe, le tabac tomberait pas terre, au mieux dans la réglette du tableau blanc. Ce n’est donc pas une pipe, c’est certain. Mais alors, qu’est-ce que c’est ? C’est peut-être, nous dit Magritte, la représentation d’une pipe ou encore, une image d’une pipe. Nuance…
Nous faisons alors le lien avec la géométrie. Ceci n’est pas une droite :
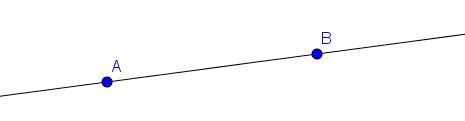
C’est une représentation d’une droite, précisément, sa représentation sous GeoGebra.
Et, ce n’est pas une question de support, ceci n’est pas une droite non plus.
insérer image d’une droite tracé à la règle sur papier blanc
C’est encore une représentation d’une droite. D’ailleurs, si l’on agrandit outrageusement le dessin à la photocopieuse, qui pourrait dire que ceci est une droite ?
insérer image d’un agrandissement
Ainsi en classe de mathématiques, nous ne travaillons, non pas sur des droites, des segments de droites ou des cercles mais sur des représentations de ces objets mathématiques. Il y a quand même une distinction que certains élèves font entre « ceci n’est pas une pipe » et « ceci n’est pas une droite ». Quand on parle de la représentation d’une pipe, on sait que l’objet existe et ce n’est bien sûr pas le cas d’une droite. Qui a déjà rencontré une droite, une vraie droite ?
Pour finir, ceci n’est pas un cercle semble dire Georges Rousse . Enfin, tout dépend du point de vue…