L’algorithmique est un domaine des mathématiques passionnant à étudier avec les élèves. On trouve beaucoup de ressources (livres, manuels, sites, etc) sur ce sujet et malheureusement on tombe souvent sur des ressources extrêmement guidées. Nous pouvons très bien faire en sorte que, lors de la présentation d’une situation aux élèves, certaines informations ne soient pas données. On les incite ainsi à s’interroger sur celles qui sont nécessaires à la résolution du problème. Un tel choix permet une meilleure dévolution de la question. Bien entendu ce principe vaut dans tous les domaines – mathématiques ou pas d’ailleurs.
Sources
Au départ nous nous inspirons largement d’un excellent article publié sur le tout aussi excellent site de l’Académie d’Aix-Marseille : Constructions de figures.
B.O.

Niveau
Nous choisissons de placer ce travail en 4e. Aucun pré-requis n’est attendu et nous imaginons que les élèves n’ont jamais encore utilisé le logiciel. Les élèves qui « Scratchent » déjà iront simplement plus vite que les autres et de nombreux prolongements sont à prévoir. C’est le cas dans toutes les activités qui tournent autour de la programmation. Certains élèves dépassent même les maîtres…
Objectifs
Introduire des notions d’algorithmique, en particulier les notions de phase d’initialisation, de boucle, de sous-programme et de variable.
Première séance : prise en mai – notion de boucle
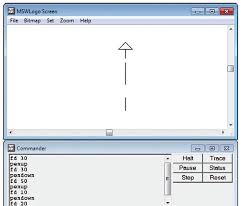
Une première présentation du logiciel est faite par le professeur qui devra montrer la scène, la palette des blocs et l’aire des scripts. A ce stade les élèves ne sont pas face à un ordinateur. Il s écoutent religieusement le professeur.
Avant de commencer on pourra supprimer le chat et le remplacer par une flèche bien plus pratique pour élaborer des dessins (notamment pour l’orientation). Cette flèche devra être réduite et recentrée.
 |
 |
 |
Cette flèche était déjà présente dans l’antique mais toujours à la mode « Tortue Logo » qui permettait dès les années 60 de programmer des figures géométriques.
|
|
|
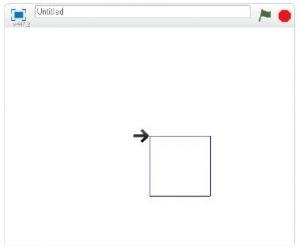
Ensuite, toujours en classe, on pourra montrer comment on peut construire un carré de côté 100. On montrera ainsi l’utilisation des blocs suivants :
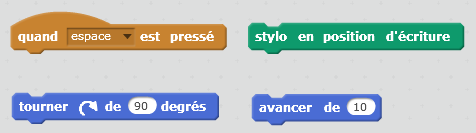
On installera alors les élèves face à un ordinateur et une liste de figures à reproduire leur sera distribuée. Pour cette première séance certains élèves parmi les plus rapides pourront commencer le motif grec.
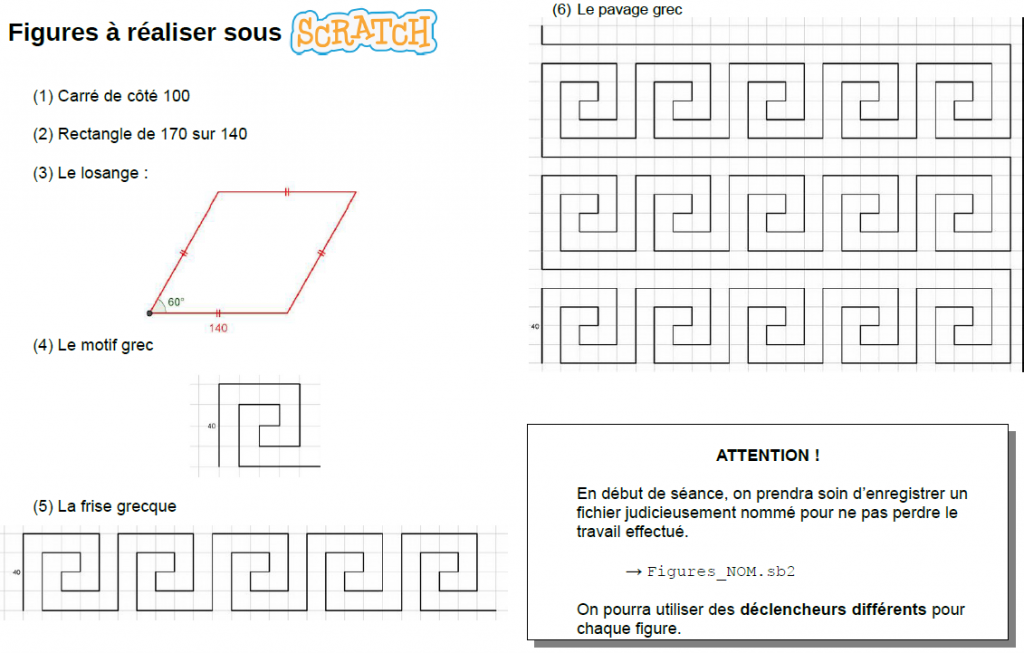
C’est au fur et à mesure des différentes constructions que le besoin d’introduire de nouvelles notions, fonctionnalités ou blocs naîtra. C’est cette idée qui sous-tend toutes les séances.
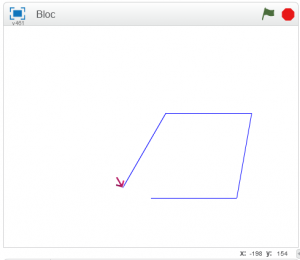
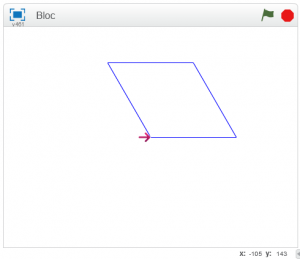
Concernant le losange, la principale difficulté est la détermination de l’angle du premier angle de rotation. Il conviendra de laisser les élèves chercher et de les inciter à essayer des angles. Ainsi, tous les élèves seront à même de valider ou d’invalider leur propre réalisation. Certains élèves obtiendront un losange symétrique. Valider cette réalisation mais faire prendre conscience aux élèves que ce n’était pas tout à fait ce qui était attendu.
|
|
|
A l’issue de cette première séance, plusieurs points seront à institutionnaliser :
- la notion d’initialisation : avant de démarrer tout programme, il y a une phase d’initialisation qui permet de « remettre tous les compteurs à zéro ».
- la notion de boucle : lorsque une partie d’un programme se répète, il convient d’utiliser une boucle (nous reviendrons sur ce principe lors de l’utilisation d’une variable).
Voici un résumé de cours possible.
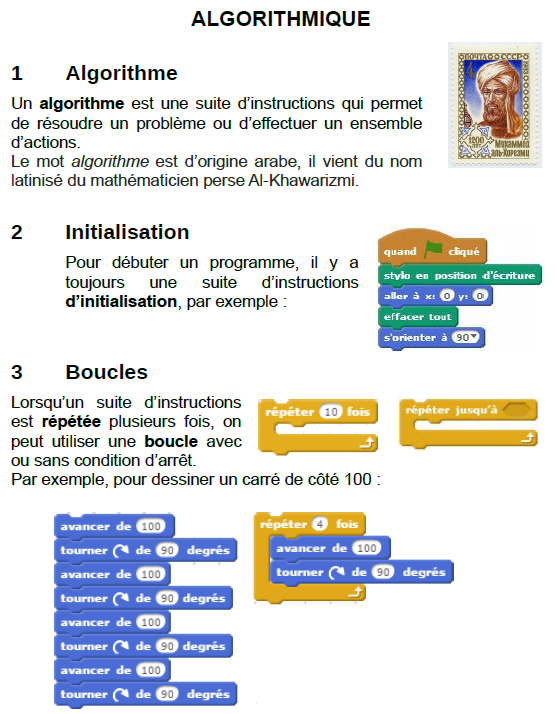
Deuxième Séance : Notion de sous-programme
Les dessins du motif grec et de la frise seront proposés dans une seconde séance. Le pavage pourra servir de prolongement pour les élèves rapides. Il conviendra de les laisser travailler en autonomie et d’institutionnaliser la notion de sous-programme qui permet d’alléger l’aire des scripts :
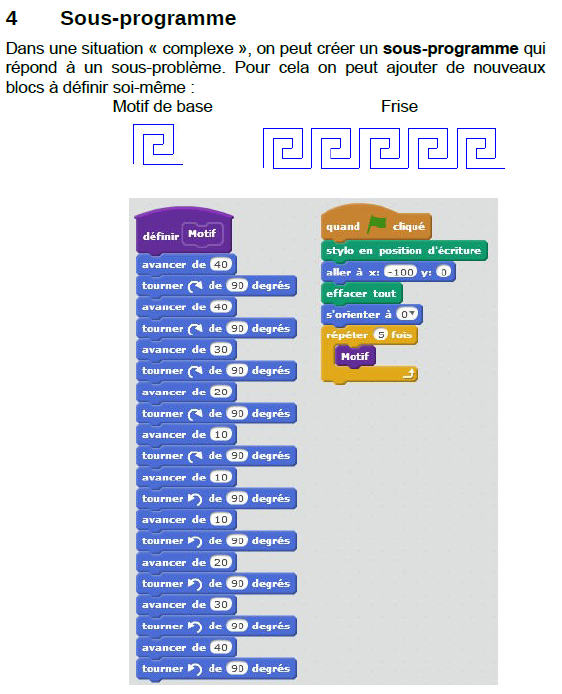
Aux élèves les plus avancés, ceux qui auront terminer le pavage, on pourra proposer d’épaissir le trait et de changer les couleurs (fond et stylo). Le résultat pourra être montré de façon à motiver l’ensemble de la classe :
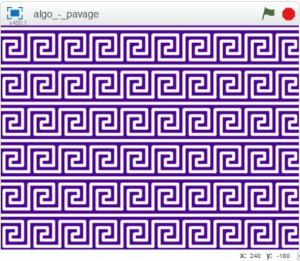
Satisfaction garantie !
Troisième séance : les variables
Il y a sans doute de nombreuses façon d’introduire la notion de variable. L’une d’entre-elles consiste, encore une fois, à créer le besoin chez les élèves par l’intermédiaire d’une figure bien choisie.
Nous proposons aux élèves de reproduire la spirale (toujours issue du site Académique d’Aix-Marseille) :
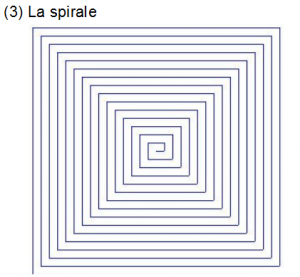
Aucune unité de longueur n’étant présente, certains élèves poseront la question de la mesure du premier petit segment au centre de la spirale. Cela fait partie des données sur lesquels ils devront réfléchir et faire le choix qui leur convient le mieux. D’autres élèves feront le choix de commencer la figure par l’extérieur. On pourra les laisser faire ou bien les engager vers une autre piste.
Rapidement, les élèves vont trouver le travail laborieux et répétitif. Ce sera alors le moment d’institutionnaliser la notion de variable : lorsque une partie d’un programme se répète, on peut utiliser une boucle. Et lorsque cette partie se répète mais que « quelque chose » varie, on peut créer puis utiliser une variable.
Montrer alors aux élèves comment on crée puis comment on utilise la variable. Les blocs mis en jeu sont :

La vidéo ci-dessous présente comment on passe d’un script sans variable à un script avec variable et pourra être mise à disposition des élèves pour la suite.
— Insérer ici le lien vers la vidéo —
Voici un résumé de cours possible. On questionnera les élèves sur les multiples avantages d’un script sur l’autre : plus court certes mais surtout dynamique.
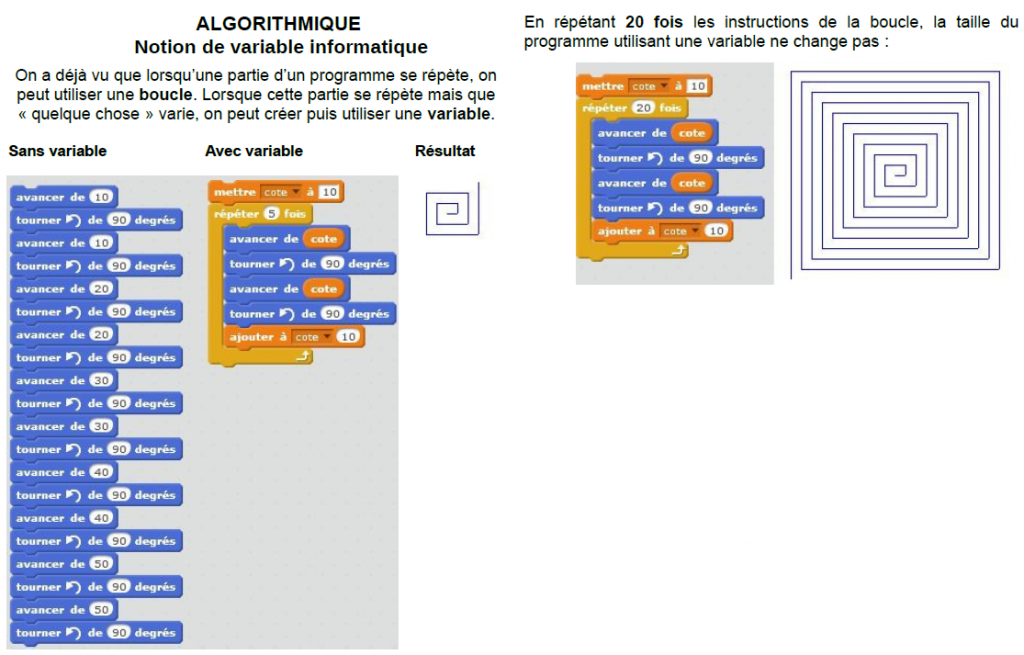
Lors d’une autre séance, remettre les élèves au travail sur une deuxième figure similaire à la spirale (dans son principe) :
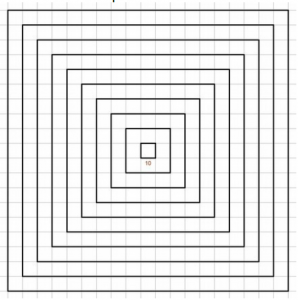
Les élèves devront, dans un premier temps produire un script simple, sans variable et se rendre compte qu’une variable est alors nécessaire. Il pourrons s’aider de la vidéo citée plus haut. A cette occasion, on pourra aussi montrer aux élèves les instructions suivantes.
![]()
Ce sera l’occasion de revenir sur le fait que « pour reculer de 10, on peut ajouter -10 ».
prolongement
Aux élèves les plus rapides, nous proposons de retravailler les pavage grec avec, comme contrainte supplémentaire, la possibilité donnée à l’utilisateur de choisir le nombre de motifs par ligne et le nombre de lignes. Pour cela on montrera les blocs suivants :
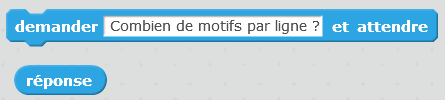
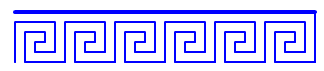
Ces élèves seront confrontés à l’utilisation de plusieurs variables. Ils devront faire un effort de recherche sur la longueur de la ligne qui permet de faire le retour au bout d’une ligne (en gras ci-dessous). Elle dépend du nombre de motifs par ligne, ainsi, on pourra faire le lien avec le calcul littéral.
Voici une vidéo qui pourra être laissée à la disposition des élèves.
Les fichiers et liens utiles
- Liste des figures
- Synthèse de cours
- Site de l’APMEP proposant des vidéos à propos de Scratch
- Le site de ressources mathématiques de l’Académie d’Aix-Marseille
Pour terminer en musique