J’ai participé aujourd’hui à une journée d’échange sur les nouveaux programmes de mathématiques du lycée. Un temps y a été consacré à ce que l’on peut appeler la « résolution de problème ». Une liste de six problèmes a été distribuée avec comme consigne de les analyser en termes de contenu mathématique, d’automatismes à travailler en amont, de différenciation des approches et en termes de coup de pouce. C’est sur ce dernier point que je voudrais revenir.
Voici l’énoncé proposé.
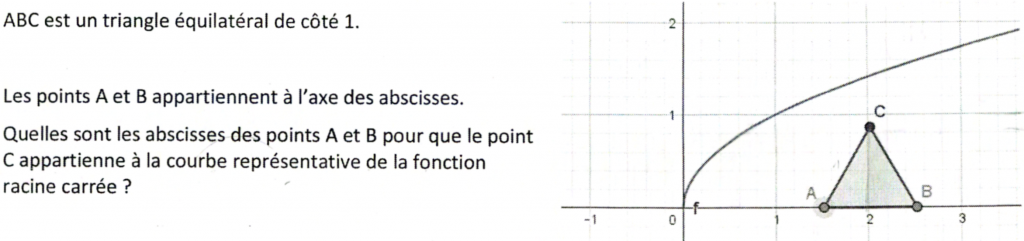
Je ne peux m’empêcher d’en modifier la question. Où placer le triangle ABC pour que C appartienne à la courbe représentative de la fonction racine carrée ? Les abscisses des points A et B sont des réponses qui peuvent venir de questions que se poseront les élèves eux-mêmes… Mais c’est de « coup de pouce qu’il est question » dans cet article et pas de la façon de poser un problème.
Je préférerais parler de « relance » pour des raisons que je vais préciser ici. Il ne s’agit pas simplement de vocabulaire mais de quelque chose de plus significatif qui a un impact direct sur le travail mathématique des élèves.
Voici un coup de pouce que proposait une collègue de l’assemblée :
Quelle est la hauteur d’un triangle équilatéral de côté a ?
C’est un intermédiaire important, c’est certain. La réponse à cette question va-t-elle aider les élèves ? Oui, dans certains cas, non dans d’autres mais là n’est pas la question. Le fait de dévoiler que c’est la hauteur du triangle qui est en jeu tue à proprement parler la tâche. N’est-ce pas aux élèves de trouver que c’est la hauteur du triangle qui détermine sa position sur l’axe des abscisses. N’est-ce pas là la part la plus intéressante de recherche ? Les élèves ne sont-ils pas capables de se poser cette question eux-mêmes ? Ce n’est pas évident, alors comment les relancer ? Voyons cela, la nature de la figure proposée a-t-elle un intérêt particulier ? Peut-on en proposer une autre ? Oui, proposons aux élèves de remplacer le triangle équilatéral de côté 1 par un carré de côté 1 puis par un rectangle de 3 sur 2 à placer dans un sens puis dans l’autre, bref de faire varier les figures et de regarder les invariants.
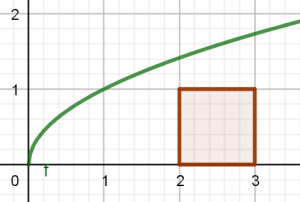
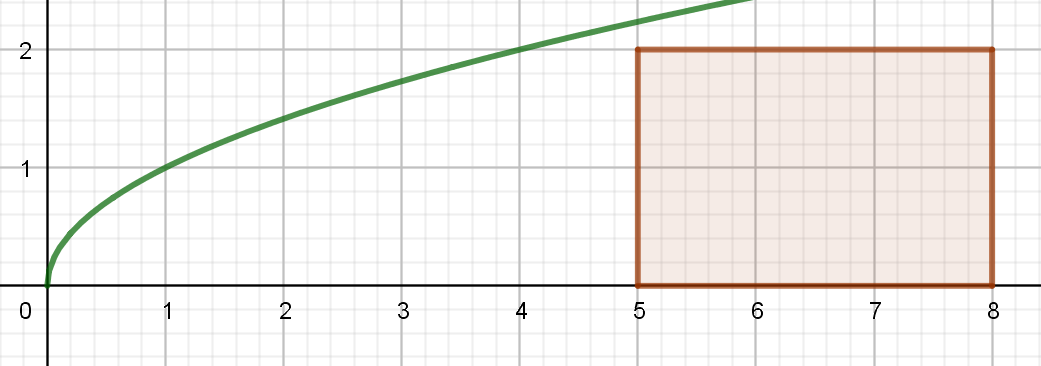
Ainsi les élèves devront comprendre que quelque soit la figure proposée, la hauteur de celle-ci joue un rôle dans cette situation (son carré en fait…). A eux maintenant de déterminer cette hauteur. Le choix de ne pas dévoiler le concept de hauteur permettra une meilleure dévolution de la tâche proposée. Faisons le pari que dans ce cas, la question soulevée par les élèves eux-même aura beaucoup plus de sens à leurs yeux et qu’ils mettront plus de cœur à y répondre qu’ils se la sont posée eux-mêmes.
Si ouvrir un problème peut s’avérer simple, en ne gardant que la dernière question et en éliminant la succession de questions intermédiaires, prévoir des relances ne peut pas se réduire à rétablir une suite de sous-questions retraçant le cheminement de pensée de l’enseignant, une relance doit permettre à un élève de faire émerger les concepts en jeu et de se poser les bonnes questions, de s’en saisir et d’y répondre.
En parlant de pouce, « Under my thumb » des Stones reprise par Pentagram, pas mal !
