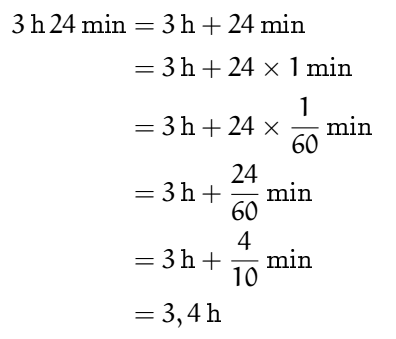On sait que les conversions de durées restent quelque chose de difficile au collège mais aussi dans la vie courante, celles des adultes. Il existe de nombreuse techniques de conversion et l’une d’entre-elles s’appuierait sur la notion de proportionnalité. C’est le cas du site MAXICOURS.com qui servira d’exemple. Il propose un cours dont l’intitulé suit.

Quelqu’un d’assez attentif remarquera que les grandeurs durée et vitesse apparaissent sans la grandeur distance. C’est donc bien sur les conversions « difficiles » que veut insister ce cours. D’emblée, MAXICOURS affiche ses objectifs où figure « comment convertir des durées ? » au même niveau de « comment convertir des vitesses ? ».

Le cours débute ainsi :

Il faut reconnaître une valeur à ce tableau qui présente non pas une égalité mais bien deux égalités pour chaque colonne/conversion. L’égalité 1 h = 60 min est présentée comme équivalente à 1 min = 1/60 h. Nous y reviendrons plus tard. En revanche, posons-nous la question ici, pourquoi ces égalités sont-elles nommées relations de proportionnalité ?. S’il s’agit effectivement d’une situation de proportionnalité, quelles en sont les deux grandeurs proportionnelles ? On notera au passage que ce tableau comporte une maladresse : 1 s = 1/60 x 1/60 h = 1/3600 h et non pas 1 s = 1/60 x 1/60 = 1/3600 h. De suite après, un exemple est proposé.

On souhaite y convertir, 2 h 14 min (que l’on trouve écrite sous la forme 2 h 14) en minutes puis en secondes. L’auteur, développe alors une technique mais celle-ci ne convoque pas la proportionnalité. Il s’agit simplement d’écrire une suite d’égalités dont nous exposons ici une version augmentée et corrigée (l’auteur, décidément maladroit, oublie une fois de plus de vérifier ses égalités).

Puis pour la seconde conversion :
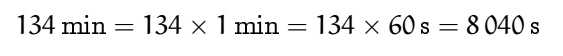
La technique est simple d’utilisation, elle met en application la première ligne du tableau relations de proportionnalité et elle est accessible à des élèves de fin de cycle 3. Bien sûr cette technique est prolongeable vers d’autres grandeurs (longueur, aires, volumes, vitesses, etc.). C’est dans le cas d’une conversion heure/minutes en heures décimales que les choses semblent se corser. L’auteur abandonne tout simplement la technique de l’exemple 1, on verra pourtant qu’elle donnerait d’excellents résultats et nous apprenons alors que « les minutes et les heures sont proportionnelles ». L’auteur propose alors un tableau de proportionnalité et applique un produit en croix. Ça marche. Cette technique fonctionne mais elle rompt avec l’exemple 1 et elle semble convoquer la notion de proportionnalité. Une question subsiste : Quel sens donner à la phrase « les minutes et les heures sont proportionnelles » ? Le tableau semble indiquer qu’il y a deux grandeurs durée. Mais les lignes de ce tableau sont étiquetées avec des unités. Il y a là une confusion (courante chez les élèves) entre grandeurs et unités.
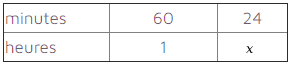
Corrigeons ce tableau :

Le coefficient de proportionnalité semble être 60. Mais pourtant les durées indiquées sont égales. C’est ennuyeux, pour nous mais pas pour l’auteur. Essayons autre chose.

Que donne le produit en croix ?
![]()
soit
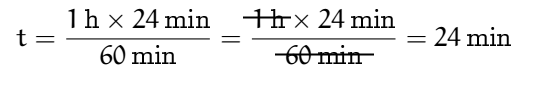
Nous voilà bien avancé ! On tourne en rond. Et ce chemin sera pris, c’est certain, par des élèves pleins de bonne volonté. Bien sûr nous aurions pu nous en sortir en écrivant :
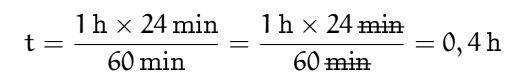
ou en utilisant le tableau précédent en écrivant :
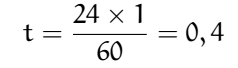
Mais on voit que la supposée situation de proportionnalité n’éclaire pas ce problème de conversion et ajoute plutôt de la confusion à la difficulté.
Pour terminer, reprenons enfin la conversion en utilisant la technique plus cohérente de l’exemple 1.