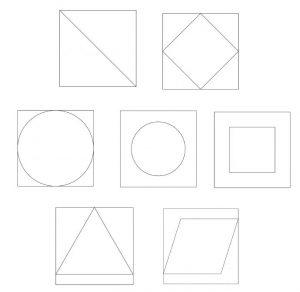
La restitution d’un travail de groupe est souvent un point délicat et donc souvent négligé. Voici ce que je propose autour de la ressource dont j’ai déjà parlé ici, Sikra. Ainsi, dans un premier temps les élèves ont analysé les dessins géométriques, ils les ont codé lors d’une travail individuel et même testé à l’aide d’un logiciel de géométrie dynamique. Ensuite par groupe de trois ils ont cherché des programmes de construction des cinq premiers motifs. Il avait à disposition, leurs figures codées et un lexique des programmes de construction.
Le déroulement
Après avoir récupéré les travaux, vient le moment de les classer et d’en sélectionner quelques-uns – inutile de tous les montrer – de façon à en tirer un bilan pertinent pour les élèves. Un diaporama est alors projeté et c’est aux élèves de « critiquer » les productions projetées. Mais attention, critiquer c’est d’abord dire une chose positive sur le travail exposé à tous. C’est important de commencer par une chose positive, le penchant naturel de la classe pousse souvent à dire ce qui ne va pas…
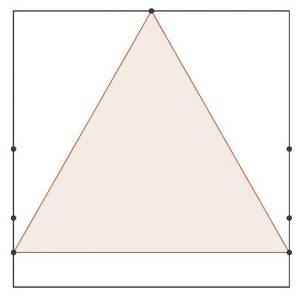
Voici les travaux choisis et ce que l’on peut en dire.

Les élèves ont un peu de mal à tirer quelque chose de positif de ce premier travail. Mais tout de même, le programme « marche », ça fonctionne, on comprends et c’est bien là le principal. Ensuite on note un effort de vocabulaire. Il faut insister de façon à valoriser ce travail qui est loin d’être inintéressant malgré son apparence pauvre. Ensuite, viennent les « critiques ». Comment peut-on améliorer ce travail ? L’écriture, la construction de phrase. Oui. Et mathématiquement ? Les notations bien entendu. Nous passons rapidement à la suite.

Le contraste est flagrant. Les compliments pleuvent. Et pourtant les mêmes soucis de notations apparaissent.
Enfin, nous terminons sur une production qui permet de se faire une idée de ce que l’on attend. Cette production fera office de corrigé.

Nous passons au deuxième motif.

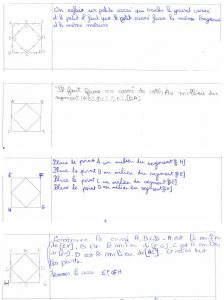
La lecture est difficile et nous en profitons pour dire aux élèves qu’il est important, non pas d’avoir une belle écriture mais une écriture parfaitement lisible. La plupart des élèves ne voit aucune amélioration possible pour ce programme. En effet, pour beaucoup d’élèves, « entre A et B » est synonyme de « milieu ». Alors nous disons qu’en mathématiques, il faut être précis et que chaque mot est important. Nous montrons le travail suivant qui est remarquable à plusieurs égards.

D’abord, les points E, F, G et H n’ont pas été définis. Un oubli sans doute… Et puis il y a cette mention des quatre angles droits au sujet du carré ABCD. A-t-on déjà vu un carré qui n’a pas ses quatre angles droits ? Il y a là une intrusion du descriptif, nécessaire lors de l’analyse du dessin et qui n’a pas sa place dans le programme de construction. Et puis il y a cette dernière phrase : tracer les segments EFGH. Les élèves ne sont pas gênés par cette tournure et nous les suivons en disant qu’il s’agit surtout d’une maladresse pour dire « le carré EFGH ».
Nous montrons ensuite une dernière production suffisamment élaborée qui permet de conclure sur ce motif. Pour la suite, nous allons parler du cercle avec le troisième motif.

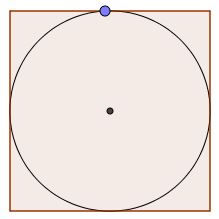
Ce que nous voulons pointer avec ce travail c’est la différence entre le lexique du matériel de géométrie et le lexique de la géométrie. Nous prenons comme exemple l’utilisation de GeoGebra car les élèves y ont déjà testé leurs figures lors d’une précédente séance. Sous GeoGebra, il n’y a pas de pointe de compas alors comment faire ? Nous faisons appel à la classe et certains élèves parlent de centre et de rayon. Nous validons et passons à la suite.

Bien sûr, les élèves n’ont pas oublié les critiques sur les notations. Nous nous arrêtons sur « le cercle qui devra toucher le milieu du carré ». Nous expliquons qu’il s’agit sans doute « du milieu du côté du carré » mais que l’expression du fait que le cercle est tangent au côté du carré est améliorable. Comment ? En montrant la dernière production.

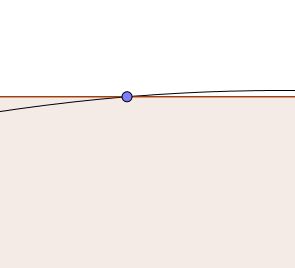
Nous voulons enfin terminer par une production qui relance les élèves Avant d’écrire un programme de construction il faut bien analyser le dessin afin d’en comprendre une possible construction. Nous questionnons alors les élèves sur la pertinence de la mesure 3 mm pour s’accorder à dire qu’il faut retourner à l’analyse du motif.

Il s’agit d’ailleurs plus d’un va-et-vient entre la rédaction du programme et sa mise à l’épreuve sous GeoGebra, le logiciel de géométrie dynamique permettant aussi de chercher une construction possible.
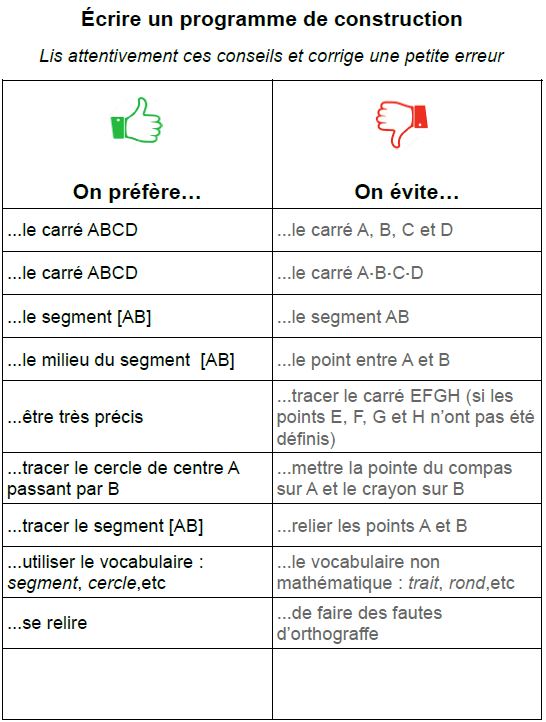
Pour terminer la séance, un bilan est distribué qui reprend et corrige les principales erreurs ou approximations vus dans les productions des élèves. Une place libre avait été prévue mais n’a pas été utilisée.
Les fichiers