Théorème de Thalès – Maths Culture

Pour faire suite à l’article sur les grandeurs, les unités et le calcul, voici une troisième situation qui montre la puissance des unités dans les calculs.

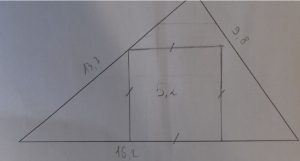
Hier soir, mon fils travaillait sur un exercice de géométrie. Je jette un œil. C’est un « classique » qui permet de montrer une utilisation concrète de la configuration croisée du théorème de Thalès. En voici la figure :

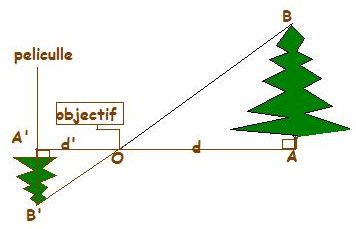
L’énoncé précise OA’ = 50 mm , AB = 12 m et OA = 25 m. Après une première question qui permet de prouver que l’on est bien dans une configuration de Thalès (le parallélisme), une deuxième question demande d’établir d’/d = A’B’/AB pour enfin, dans une troisième question déterminer la distance A’B’, taille de l’arbre sur la pellicule qui est, en passant une distance bien plus facilement mesurable que la hauteur de l’arbre. Mais le sujet n’est pas là. On voit que l’utilisation de l’égalité de la deuxième question, va poser (ou devrait poser) des problèmes d’homogénéité des unités. On a d’une part des mètres et d’autre part des millimètres.

Une première résolution consisterait à convertir toutes les distances dans une même unité, par exemple le mètre.

d’ = 50 mm = 0,05 m
d = 25 m
AB = 12 m
On obtient donc :

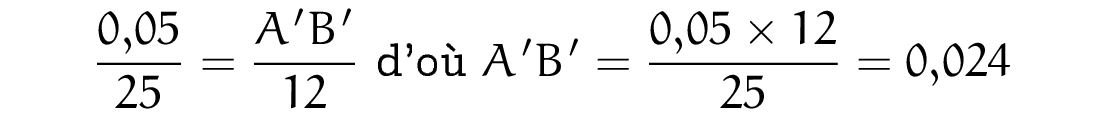
On conclut alors que l’image mesure 0,024 m soit 24 mm.

Une deuxième solution possible montre que ces changements d’unités ne sont pas nécessaires. En s’affranchissant entièrement des unités, on obtient les égalités suivantes :

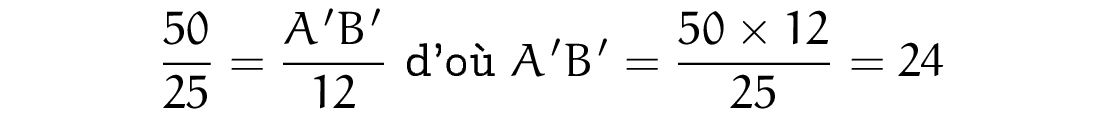
Et puis, que faire de ce résultat sans unité ? On peut toujours lui coller des mm, cela passera sans doute mais on sent bien que derrière ce calcul, il y a un tour de passe-passe non dévoilé.

C’est la troisième solution qui dévoile ce tour. Écrivons simplement les unités dans ces calculs :

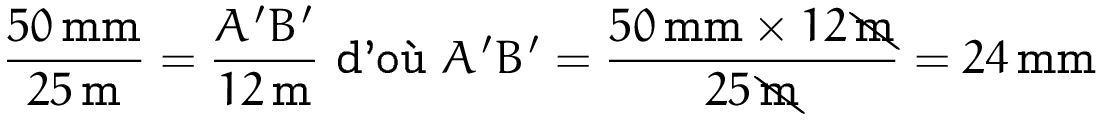
Par la « simplification par m », simplification bien connue des élèves dans le cadre numérique mais plus rarement dans le cadre des grandeurs, la distance A’B’ se voit affecter naturellement (en fait, algébriquement) son unité, le mm.

Bien sûr, on peut aussi calculer un coefficient de proportionnalité :

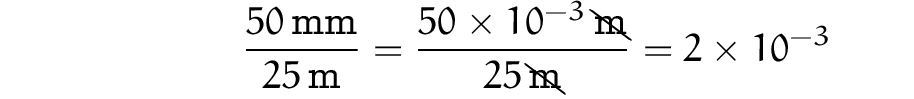
C’est-à-dire, une grandeur sans unité soit un nombre, que l’on applique aux 12 m.

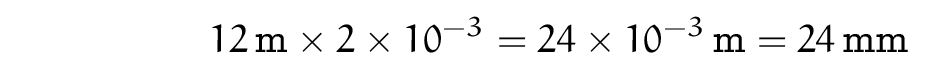
Et retrouver à peu de frais les 24 mm de l’image.

Objectif

Découvrir l’homothétie en deux séances

ÉNONCÉ

Niveau

Fin de cycle 4, 3ème

Pré-requis

Avoir déjà utilisé GeoGebra
Avoir déjà étudié un même type de tâche (inscrire une figure dans une autre), par exemple :

De même, avoir déjà travaillé une question d’agrandissement, par exemple :

Déroulement

Commencer par montrer une figure dynamique sous GeoGebra afin de faire comprendre à la classe qu’il ne s’agit pas de reproduire une figure (statique) particulière mais que la construction doit pouvoir fonctionner sur tous les triangles possibles.
Dire aux élèves qu’ils vont devoir comprendre comment est construit le carré inscrit dans le triangle et qu’une fois la construction établie, ils pourront la réaliser sous GeoGebra.
Distribuer l’énoncé et mettre les élèves au travail : papier/crayon. Cette étape est importante, les élèves doivent prendre conscience de la difficulté de la construction. Comment faire en sorte que deux sommets soient sur deux côtés du triangle et que les deux autres sommets soient sur le même troisième côté ? On pourra distribuer des « figures pour comprendre ». Ce sont des figures déjà réalisées sur lesquelles les élèves peuvent effectuer des tracés, repérer des alignements, mesurer, bref explorer.

Relances / difficultés

Les élèves vont produire des figures qu’ils ont réalisés à tâtons. En montrer une à la classe via un vidéoprojecteur. Elle pourra sembler justes à certains et une discussion de classe permettra de l’invalider après en avoir aussi montré les aspects positifs. Il faudra alors relancer la classe pour la faire sortir de cette situation de blocage.
Une relance importante consiste à abaisser une contrainte :

Construire un carré avec un sommet intérieur au triangle	Construire un carré avec un côté parallèle à un côté du triangle

Une fois la contrainte abaissée, la figure est relativement simple à construire. Questionner alors les élèves sur la taille du carré ainsi construit. Le carré solution est un agrandissement du « petit » carré, comment le construire ? Peut-on construire des carrés de plus en plus grand ? Le carré pouvant même dépasser le carré solution. Une fois plusieurs carrés construits, peut-on trouver des alignements (sommets des carrés) ? Ces relances ont pour but d’obtenir des carrés homothétiques afin d’obtenir un sommet du carré solution :

Une fois la construction réalisée par tous, lors d’une deuxième séance, passer sous GeoGebra. On pourra limiter les outils avec une version de GeoGebra « allégée » :

Institutionnalisation

Voici un bilan possible qui montre les aspects dynamiques de l’homothétie qui devient un outil pour construire.

Prolongements

Lors de la séance sous GeoGebra, vérifier que la construction fonctionne dans tous les cas (lorsqu’un des angles de la « base » est obtus). Si ce n’est pas le cas demander de corriger, il faudra alors considérer les droites qui supportent les côtés du triangle et non pas seulement les segments.
Proposer de construire des carrés inscrits à l’infini (dans les trois triangles restants) ou de construire les trois cercles inscrits dans les trois triangles restants (Sangaku) :

Conclusion