Que faut-il retenir du cours sur les systèmes oscillants selon les connaissances et savoir-faire exigibles du programme officiel ?

Dans cet article comme dans tous les articles de mécanique, les vecteurs sont notés en gras.

D’abord, quelques faits autour du pendule simple

Définir un pendule simple.

Un pendule simple, est tout simplement :

• Un objet ponctuel suspendu à un point fixe par un fil inextensible.

C’est à dire ? une petite masse accroché à un fil de longueur fixe, sans élasticité.

Qu’est-ce que cela veut dire ponctuel ? Pour un mathématicien, ça veut dire infiniment petit (ils ont des définitions du genre : vous imaginez tout ce que vous avez de plus petit et c’est encore plus petit). Bien sûr qu’il n’y a pas grand chose qui vérifie le fait d’être « ponctuel » (hormis peut-être les particules élémentaires) mais pour nous en mécanique, on considérera que la masse est « ponctuelle » du moment que ses dimensions sont plus petites que la longueur du fil (et pas du moment qu’elle arrive à l’heure…).

Justifier la position d’équilibre dans le cas d’un pendule simple.

Comme le solide est soumis à 2 forces (le poids et la tension du fil), sa position d’équilibre est lorsque ces deux forces se compensent : lorsque le fil est vertical. Si l’objet est dans cette position sans vitesse, comme la somme des forces est nulle, l’accélération l’est aussi et le solide perdure dans cette position.

Définir l’écart à l’équilibre, l’abscisse angulaire, l’amplitude, la pseudo-période, la période propre et les mesurer sur un enregistrement.

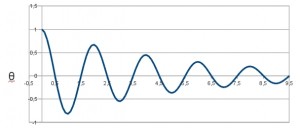
Si l’on écarte l’objet de la position d’équilibre, le fil forme un angle avec la verticale. Cet angle, généralement noté ?, est une mesure de l’écart à l’équilibre. On l’appelle abscisse angulaire. Lorsque l’on trace les variations de cet grandeur en fonction du temps, on trouve quelque chose comme ça :

Qui s’étudie de la même façon que la dernière fois que nous avons rencontré ce genre d’évolution temporelle : avec le dipôle RLC. Sur le schéma ci-dessus, l’amplitude des oscillations diminue progressivement, il s’agit d’un régime apériodique. La pseudo-période se trouve en mesurant le temps mis pour que la courbe passe 2 fois par zéro dans le même sens, ici : 2 secondes.

Enoncer la loi d’isochronisme des petites oscillations.

Une petite loi toute simple à apprendre et à comprendre :

• Pour des oscillations de faible amplitude (on considère généralement ? inférieur à 15°), la période est indépendante de l’amplitude.

Ce qui veut dire que le pendule met toujours le même temps pour parcourir un aller-retour lorsque l’amplitude n’est pas trop élevée.

Savoir comment un système peut atteindre un régime apériodique.

Dans le cas idéal où il n’y a pas de frottement, le pendule oscille indéfiniment autour de sa position d’équilibre et l’amplitude reste toujours constante. Dès lors qu’il y a des frottements, il y a amortissement et l’amplitude des oscillations se met à diminuer. C’est le régime apériodique.

Savoir que dans le cas d’un amortissement faible, la pseudo-période est voisine de la période propre.

Tout est dit. Que dire de plus ?

Pour un pendule simple, justifier la forme de l’expression de la période propre par analyse dimensionnelle.

Ah, c’est là que les choses deviennent intéressantes. Pour le pendule simple, la période propre s’exprime T₀=2.pi.?(l/g) [2 pi racine de l sur g] où l est la longueur du fil.

Cette expression est homogène, c’est à dire que l’unité du membre de droite est égale à l’unité du membre de gauche.

En effet, g s’exprime en N/kg mais également en m/s² (mais si, rappelez-vous de ce que l’on a vu dans la chute libre, a=g donc g a la même unité que l’accélération). Ainsi, l/g est homogène à m/(m/s²)=s². La racine de l/g est donc homogène à des secondes. Comme 2.pi n’a pas d’unité, 2.pi.?(l/g) est bien homogène à du temps. CQFD !

À partir d’une série de résultats expérimentaux, vérifier la validité de l’expression de la période propre d’un pendule simple.

Il s’agit en fait de vérifier l’expression précédente. Pour cela, on procède généralement en mesurant la période propre pour plusieurs longueurs de fils. On obtient alors des valeurs de T₀ en fonction de l. Pour vérifier la validité de l’expression T₀=2.pi.?(l/g), il ne reste plus qu’à tracer T₀ en fonction de ?(l). On devrait trouver une droite de pente 2.pi/?(g)

Et puis tout sur le système solide-ressort

Connaître les caractéristiques de la force de rappel exercée par un ressort.

La force de rappel d’un ressort est proportionnelle à l’élongation et dirigée vers la position de repos. Si l’on note l₀, la longueur du ressort « à vide » c’est à dire sans contrainte, la force de rappel est égale à k.(l-l₀) où k est la constante de raideur du ressort, qui s’exprime en N/m. Le point d’application de cette force est le point d’attache du ressort au solide.

Dans le cas d’un solide accroché à un ressort, celui-ci s’allonge de sorte à compenser le poids. Cela permet de mesurer la constante de raideur k. En effet, dans la position d’équilibre, les forces se compensent. Le poids est vertical dirigé vers le bas, tandis que la force de rappel du ressort est verticale dirigée vers le haut. Les normes des 2 vecteurs sont égales : m.g=k.(l-l₀) ce qui permet de calculer k=m.g/(l-l₀).

Dans le cas d’une configuration horizontale, on note généralement x, l’écart à la position d’équilibre du centre d’inertie de l’objet. Lorsque x est nul, le ressort à sa longueur à vide et la force de rappel est nulle. Dans ces conditions, la force de rappel du ressort s’exprime : F=-k.x.i où F est l’expression vectorielle de la force de rappel et i le vecteur unitaire. On peut vérifier que cette expression marche bien dans les 2 sens : si x est positif, F_x est négatif dirigée de sorte à diminuer x; si x est négatif, F_x est positif, de sorte à augmenter x. Ainsi F est toujours dirigé de sorte à ramener le solide vers la position x=0.

Appliquer la deuxième loi de Newton au solide et effectuer la résolution analytique dans le cas d’un dispositif oscillant horizontalement.

Voilà le coeur du problème, ce qui est technique et qu’il faut être capable de restituer :

1. On pose le problème :
   Envisageons un solide relié à un ressort. à t=0, on éloigne le solide de la position d’équilibre, et on le lache sans vitesse initiale. Notons u_x le vecteur unitaire horizontal, et prenons x=0 à la position d’équilibre, u_z le vecteur unitaire verticale. Ce solide est soumis à 4 forces :

1. Le poids : P=-mg.u_z
2. La réaction du support : R=R.u_z
3. La force de rappel du ressort : F=-k.x.u_x
4. Une force de frottement visqueux (optionnel) qui s’oppose au mouvement : f=-?.v

• On écrit la seconde loi de Newton : P+R+F+f=m.a
  Le mouvement étant horizontal, a=a_x.u_x et v=v_x.u_x
  Ainsi, le seconde loi de Newton peut se réécrire : -mg.u_z+R.u_z-k.x.u_x-?.v_x.u_x=m.a_x.u_x
• On regarde ce qui se passe sur chaque axe :
  Ce qui donne selon u_z : R-m.g=0 ? la réaction du support compense le poids
  et selon u_x : -k.x-?.v_x=m.a_x ? m.a_x+?.v_x+k.x=0
  Dans le cas où l’on néglige les frottements (ce qui est demandé au niveau du programme), on trouve l’équation du mouvement, en se rappelant que a_x=d²x/dt² : m.d²x/dt²+k.x=0
• On résout l’équation différentielle :
  On retrouve une équation d’un genre que l’on a déjà vu dans le cas du dipôle RLC. La solution est de la forme : x(t)=X_m.cos(2.pi.t/T₀+phi)
  Nous verrons au point suivant que la signification de chacun des termes de cette expression doit être connue.
  Pour la suite, c’est du classique, on l’a déjà fait plusieurs fois en électricité : après avoir dérivé 2 fois x(t) et injecter l’expression de d²x/dt² et de x(t) dans l’équation différentielle, on obtient : -m.(2.pi./T₀)².X_m.cos(2.pi.t/T₀+phi)+k.X_m.cos(2.pi.t/T₀+phi)=0 qui n’est possible à chaque instant que si -m.(2.pi./T₀)²+k=0 soit T₀=2.pi.?(m/k)
• On regarde ce que ça donne avec les conditions initiales :
  x(0)=X₀ ? X_m.cos(phi)=X₀
  dx/dt(0)=0 ? X_m.sin(phi)=0 ? phi=0 et donc  X_m.cos(phi)=X₀
• On recolle tous les morceaux :
  La solution est x(t)=X₀.cos(2.pi.t/T₀) avec T₀=2.pi.?(m/k)

 

Connaître la signification de tous les termes intervenant dans la solution de l’équation différentielle et leur unité.

L’équation différentielle que nous avons obtenue est : m.a_x+?.v_x+k.x=0

• m.a_x : correspond à l’inertie, c’est la produit de la masse (en kg) par l’accélération (en m/s²)
• ?.v_x : correspond aux frottements fluide, c’est le produit du coefficient de frottement (en N.s/m) par la vitesse (en m/s)
• k.x : correspond à la force de tension du ressort, c’est le produit du coefficient de raideur (en N/m) par la position du solide (en m)

Connaître et savoir exploiter l’expression de la période propre, vérifier son homogénéité par analyse dimensionnelle.

L’expression de la période propre est T₀=2.pi.?(m/k). Savoir exploiter cette relatin veut dire être capable de calculer T₀ lorsqu’on vous donne m ou k, ou bien déduire k si l’on mesure T₀ et m (k=(2.pi/T₀)².m).

Pour vérifier l’homogénéité de la relation, il faut se rappeler que k est en N/m et que des Newton sont équivalent à des kg.m/s². En effet, les forces (en N) sont égales au produit d’une accélération (en m/s²) par une masse (en kg). Ainsi, m/k a pour unité : kg/(kg.m/s²)=s². La racine de m/k est donc homogène à des secondes. Pour 2.pi, ce n’est qu’un coefficient numérique sans unité.

Savoir que la résonance mécanique se produit lorsque la période de l’excitateur est voisine de la période propre du résonateur.

Ce point concerne la résonnance, le phénomène qui apparaît lorsqu’on couple un excitateur avec un système oscillant (appelé dans ce cas résonateur) : l’amplitude du mouvement du résonateur est maximale lorsque la fréquence de l’excitateur est égale à la fréquence propre du résonateur. Autrement dit, lorsque la période de l’excitateur est égale à celle du résonateur. Tout est dit dans l’énoncé de la connaissance exigible.

Savoir que l’augmentation de l’amortissement provoque une diminution de l’amplitude.

Sans amortissement, le phénomène de résonance entraîne la destruction du résonateur (voir la vidéo de l’hélicoptère à la fin de l’article la résonance en vidéo). L’amortissement modère le phénomène et une augmentation de l’amortissement provoque une diminution de l’amplitude.

Connaître des exemples de résonance mécanique.

L’exemple classique est constitué d’un système excitant un système solide-ressort verticale (voir par exemple le sujet Réunion 2003 – merci labolycee.org) mais on trouvera d’autres exemples (plus ou moins classique) dans l’article la résonance en vidéo.