
La méthode des cycles chinois est une technique d’enseignement d’inspiration taoïste, prémisses sans doute passablement rédhibitoires mais à l’heure du désamour sans cesse croissant entre les élèves et les mathématiques, et d’un niveau qui ne ferait que baisser, elle recèle peut-être des qualités intéressantes.
Dans cette méthode les notions enseignées sont d’abord contextualisées au travers d’activités motivantes dans une progression circulaire qui part de la pratique pour aller vers la théorie et finalement retourner à la pratique.
Elle évite ainsi l’écueil d’une lecture linéaire du programme, ce squelette auquel le professeur doit ajouter la chair, où toutes les notions s’enchaîneraient sans finalement vraiment prendre sens pour les apprenants.
Ce cycle de contextualisation, décontextualisation, recontextualisation se déroule dans une alternance précisément définie de phases de recherches, de synthèses et d’apprentissages et parallèlement de séances alternativement dirigées ou non dirigées.
Cette succession va apporter différents éclairages sur un même concept, ce qui va favoriser sa compréhension et son assimilation et permettre à chaque élève de trouver sa place au sein d’un rituel rassurant.
Elle va permettre ainsi l’acquisition en douceur, mais solidement ancrée, dans une évolution lente, simple et naturelle, de toutes les théories.
Vous trouverez, ci-dessous, des liens vers tous les documents nécessaires pour mettre en place des activités variées et intéressantes dont les formulations sont accessibles à tous, même si leur résolution peut se révéler extrêmement complexe: Construction de maquettes, décryptage, courses d’orientations, cartes au trésor, jeux et énigmes, sondages, etc. qui suscitent toujours beaucoup d’enthousiasme et rendent aisée la mise au travail.
La méthode s’articule autour de deux cycles l’un pour structurer les séquences et l’autre pour les séances.
Le cycle des séquences
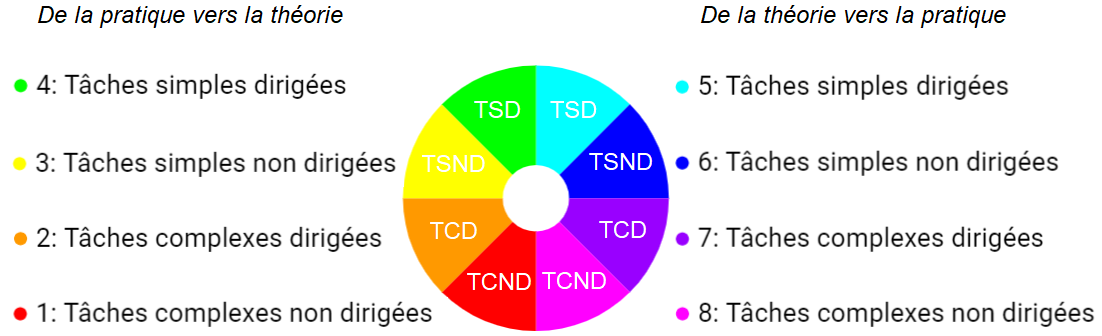
La progression pratique-théorie-pratique est déjà bien connue en pédagogie mais cette méthode se caractérise par une trame très précise. Chaque chapitre comporte huit séances qui se succèdent invariablement dans cet ordre:
Il ne faudrait surtout pas confondre cette progression avec celle qui est traditionnellement proposée dans la plupart des manuels scolaires et qui, en substance, est souvent proche de celle-ci: Activités d’approche, cours, exercice d’application, exercices plus approfondis, problèmes, TD, tâches complexes et problèmes ouverts, à quelques variantes près.
Elle n’a en réalité pas grand chose à voir. Les activités d’approche sont souvent artificielles car dirigées vers un objectif précis qui vient trop vite. Le cours arrive immédiatement après, dans la même séance en général, sans laisser le temps de maturation qui permettrait de s’imprégner des nouvelles notions. Elle suppose généralement une réactivité qui reste bien souvent illusoire pour des apprenants qui n’ont pas encore la vision panoramique de leur enseignant. Ici la progression est beaucoup plus lente. Les mêmes notions vont être vues plusieurs fois de suite, pendant plusieurs séances, sous plusieurs angles différents, de plus en plus focalisés et théoriques. Un travail de recherches alternativement individuelles et collectives va progressivement amener à la théorisation, le cours ne viendra qu’entériner ce qui a déjà été compris.
L’ autre principe sous-jacent de ce cycle, en plus de l’ancrage sur la progression pratique-théorie-pratique, est essentiellement une recherche de diversité et d’équilibre entre toutes les activités.
- La moitié du temps de la séquence va de la pratique vers la théorie, l’autre moitié dans le sens inverse,
- La moitié du temps est consacrée aux tâches complexes, l’autre moitié aux tâches simples,
- La moitié des séances sont dirigées et pendant l’autre moitié les élèves sont autonomes dans leurs recherches.
Cet équilibre va permettre à chaque élève d’y trouver tour à tour son compte, de celui qui n’est à l’aise que lors de séances magistrales rigoureuses, qui aime reproduire ce qu’on lui a montré à celui qui ne s’épanouit que dans la liberté, l’imagination ou le refus des cadres trop rigides.
On peut aussi traduire le premier diagramme avec le vocabulaire suivant:
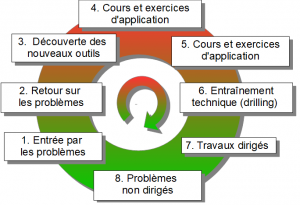
Entrée par les problèmes
La séquence commence par un ou plusieurs problèmes complexes, ouverts ou compliqués, dans lesquels se dissimulent des outils encore inconnus des élèves et qui constitueront l’essentiel de la séquence. Tout ce qui va suivre est presque entièrement inclus dans cette séance.
L’ activité, par l’intérêt qu’elle présente, suscite rapidement l’adhésion des élèves.
Il n’est peut-être pas inutile de rappeler qu’une tâche complexe est, pour simplifier, une tâche qui nécessite plusieurs étapes, mobilise plusieurs connaissances et peut être résolue de diverses façons. « Complexe » ne devant pas être confondu avec « compliqué ». À l’inverse une tâche simple peut être redoutablement difficile.
Retour sur les problèmes
On revient sur les problèmes en reprenant les différentes procédures utilisées par les élèves puis on introduit de nouveaux outils plus performants inventés par les mathématiciens.
Malgré son côté redondant cette séance est généralement bien acceptée par les élèves. Elle est importante pour structurer l’activité de recherche de la séance précédente, s’assurer que le plus grand nombre d’élèves ont bien compris et mettre en lumière les outils mathématiques qu’il va falloir apprendre à maîtriser.
Découverte des nouveaux outils
On propose des exercices simples utilisant les nouveaux outils mais sans guider les élèves.
Ces outils ne sont donc pas parachutés d’on ne sait où comme de nouvelles notions vides de sens qu’il va falloir apprendre mais bien perçus pour ce qu’ils sont en réalité, des instruments utiles pour résoudre des problèmes.
Cours et exercices d’application
Les outils, désormais familiers et globalement bien acceptés, sont maintenant rigoureusement formulés par le professeur et immédiatement appliqués dans des exercices très simples.
Les élèves recopient les leçons, à la maison … Ce travail de copie manuscrite est très important pour la plupart d’entre eux dans le processus de mémorisation.
Entraînement technique
Les élèves se familiarisent avec les nouveaux outils et développent leur maîtrise technique en essayant de faire le maximum d’exercices d’application directe.
Travaux dirigés
On recommence à résoudre des problèmes, mais cette fois-ci en utilisant les nouveaux outils. Les élèves sont guidés pas-à-pas.
En général, un des exercices de ce document se trouve dans l’évaluation finale.
Problèmes non dirigés
C’est l’aboutissement (l’apothéose ?), de toute la séquence. Les élèves sont désormais aptes à revenir sur le problème initial de la première séance armés de nouveaux outils bien plus performants ou de résoudre seuls des problèmes d’un niveau de complexité et de difficulté beaucoup plus élevés que lors de la séance initiale et peuvent ainsi mesurer tout le travail accompli depuis le début de la séquence.
Le cycle des séances
Le rituel d’une séance est très vite adopté par les élèves.
Chaque séance est découpée en cinq périodes de durées égales. Il est fondamental de veiller à ce qu’aucune phase n’empiète sur les autres.
Consacrer trop de temps à corriger les exercices, par exemple, limiterait nécessairement les phases suivantes qui ne peuvent être utiles que si elles sont suffisamment longues.
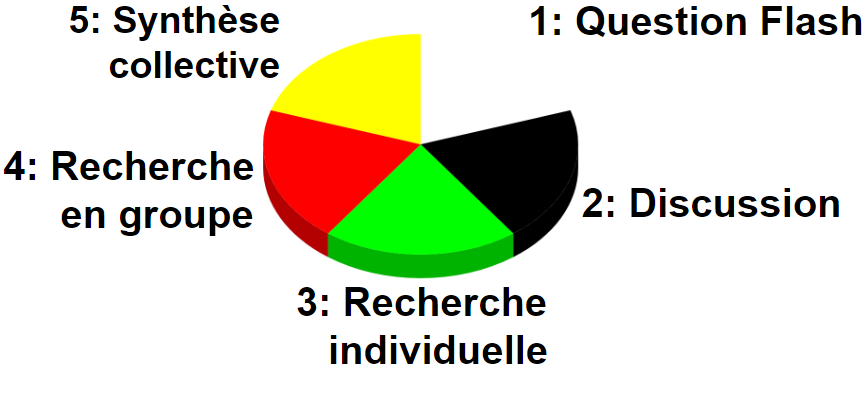
Question flash

La séance commence par une petite interrogation très rapide sur les notions récemment étudiées.
Pendant l’interrogation un groupe d’élèves, choisis lors de la précédente séance, vient au tableau pour y écrire ses propositions de corrections des exercices qui étaient à finir pour cette séance.
Discussion

Des élèves viennent au tableau corriger les questions flashs.
Ensuite, le groupe qui est passé au tableau lors de la précédente phase pour y écrire ses corrections, y retourne afin de les expliquer. Le professeur intervient mais laisse , dans la mesure du possible, les élèves, ceux au tableau et les autres, s’exprimer le plus possible, et interagir entre eux. Idéalement, il se positionne uniquement en tant qu’observateur expert, pose des questions, corrige les erreurs, les imprécisions, donne des indications sur la rédaction, etc. Il introduit ensuite la phase suivante en indiquant les objectifs attendus et éventuellement en présentant certaines techniques. La question flash sert d’ailleurs souvent comme support pour introduire le reste de la séance.
Recherche individuelle
Tout le travail de la séance est présenté simultanément. Les élèves doivent travailler, seuls, dans le plus grand silence, dans l’ordre proposé et à leur rythme. Pendant cette phase le professeur se déplace dans les rangs afin de répondre aux questions, aider, solliciter, encourager.
Les documents comportant une série d’exercices (généralement lors des séances 2 à 7) sont structurés en trois parties de difficulté croissante. La première partie, en général le recto de la feuille) devrait être faite par tous les élèves, elle est, la plupart du temps, intégralement corrigée lors de la dernière phase (Synthèse). La seconde partie doit être largement abordée et de préférence terminée par la majorité de la classe. Elle est, en règle générale, à terminer pour la séance suivante. La troisième partie est destinée aux élèves les plus avancés, il s’agit régulièrement d’un bonus pris en compte dans l’évaluation des élèves.
Recherche en groupe

A la fin de la phase précédente les élèves se sont appropriés les problèmes, ils ont trouvé des pistes qui vont se compléter. Cette fois-ci l’enseignant s’adresse aux groupes plutôt qu’aux élèves individuellement. Pendant cette phase un des groupes passe au tableau pour y écrire ses solutions, sans commentaires à ce stade.
Synthèse
Les élèves du groupe désigné viennent au tableau expliquer leur correction des exercices . Ils sont interrogés par les autres élèves et par l’enseignant qui apporte une nouvelle fois sa parole d’expert.
Ce dernier conclut ensuite la séance, demande aux élèves ce qu’ils ont le sentiment d’avoir appris, et indique les exercices à finir pour la prochaine après avoir donné des pistes de travail.
Exemples d’activités
En 6ème
Le temple d’Horus

Les élèves sont des scribes égyptiens et doivent construire une maquette. Mais comment faire à une époque où ni le mètre ni l’écriture décimale n’ont été inventés ?
C’est l’objet de discussion avec les élèves qui vont proposer divers procédés. On retiendra l’usage d’une partie du corps: la paume, et des fractions, seule solution pour l’instant.
C’est donc l’occasion d’introduire et de travailler sur les fractions, historiquement le premier outil pour mesurer les quantités non entières. L’écriture décimale apparaîtra progressivement à travers les premières séquences, les élèves progressant dans l’Histoire et la géographie comme des voyageurs du temps.
Le village des 6èmes
Cette activité occupe deux séquences différentes, lors de la première les élèves construisent une maquette de maison à partir d’un plan qu’ils ont créé. (Travail sur les solides, les échelles, les conversions d’unités, etc.)

Lors de la seconde séquence les élèves sont à la fois clients, ils doivent acheter les murs et les sols de leur maison, et fournisseurs des autres élèves. (Travail sur les aires et les périmètres).

En 5ème
Tours de magie
Les élèves apprennent à faire et créer des tours de magie avec des nombres. Le secret résidant dans la maîtrise de certaines notions élémentaires de l’écriture littérale.
Exemple:

Codes secrets
Comment déchiffrer un texte comme celui-ci qui semble réfractaire aux analyses élémentaires ?

Cette activité va être un prétexte pour l’étude statistique, le calcul de pourcentages, la construction de diagrammes en bâtons ou circulaires, etc.
Maquette
Le château de Guédelon pour travailler proportionnalité, échelles, circonférence du cercle, construction de cylindres et de cônes.

En 4ème
Le théorème de Pythagore
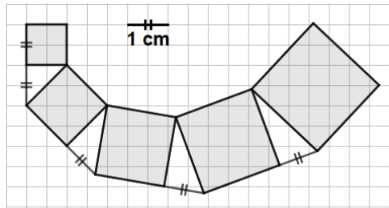
On demande de dessiner un carré de 1cm², puis de 2 cm², 3 cm², etc. Sur une feuille quadrillée (5mmx5mm). Ce problème n’est pas aussi simple qu’il n’y paraît et va être l’occasion de découvrir le carré et la racine carrée d’un nombre, approximer une racine carrée par tâtonnement (pour certains élèves cela sera même l’occasion de revoir l’ordre en écriture décimale). On arrive au théorème de Pythagore en découvrant que les seuls carrés que l’on peut dessiner en utilisant les nœuds du quadrillage peuvent toujours s’exprimer comme la somme de deux carrés parfaits.
Une des solutions, qui n’apparaîtra qu’à la 8ème séance, étant celle-ci:
Course d’orientation
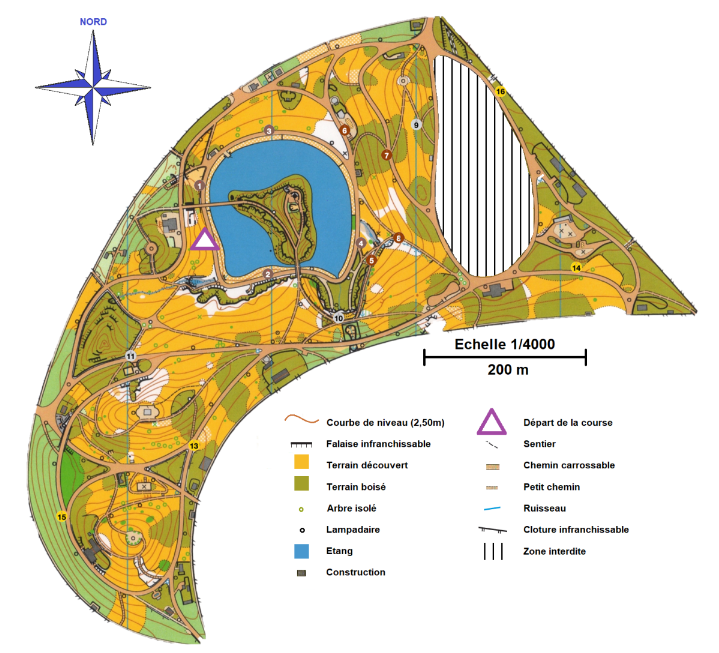
C’est une activité très riche. Les itinéraires sont conçus par groupe en fonction de leur VO2max, c’est l’occasion de travailler sur les échelles, les vitesses (et la proportionnalité en général), la lecture de carte, de graphiques, calculer avec des durées, …
Initiation aux équations
Il s’agit ici de trouver le prix des fleurs, sachant que les deux compositions ont le même prix.
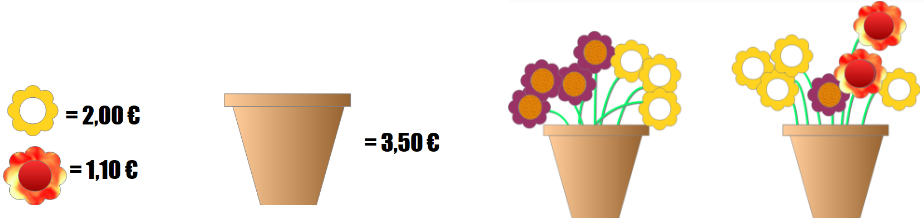
Et là, de trouver le poids des boules.
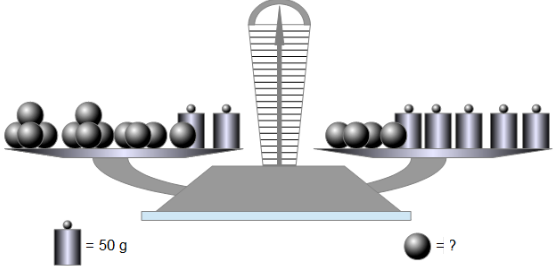
On peut résoudre ces problèmes sans faire appel aux équations, et c’est ce que vont faire les élèves, et ils vont redécouvrir et développer eux-mêmes les procédures classiques de résolution. L’écriture littérale va apparaître pour eux comme un outil très pratique pour accélérer la rédaction de ces procédures.
En 3ème
Mesurer le collège.

Les élèves cherchent le maximum de techniques pour mesurer la hauteur du bâtiment. Le théorème de Thalès arrive tout naturellement.
Les boîtes de sucre
Comment construire la boîte la plus volumineuse possible à partir d’une feuille A4, en suivant quelques contraintes sur la forme du patron. C’est une introduction sur les fonctions, les tableurs, et un travail sur l’écriture littérale qui prend ici une signification très claire.
Les élèves commencent par faire des découpages, puis comprennent à un moment donné qu’il vaut mieux utiliser des modélisations et des calculs, modélisations qui commencent sur le cahier puis aboutissent sur les ordinateurs.
Probabilités
Elles sont toujours introduites à partir de jeux de hasard auxquels jouent réellement les élèves (il ne s’agit pas d’exemples théoriques) afin de découvrir par eux-mêmes plusieurs propriétés.
Sur le plateau ci-dessous, par exemple, ils doivent miser sur une case, le gain étant déterminé par une carte tirée au hasard. Les mises rapportent plus ou moins de points (par exemple la mise trèfle rapporte 4 points, alors que la mise Roi en rapporte 8). Les élèves réalisent progressivement que le hasard obéit à certaines règles, et que certaines intuitions largement répandues sont totalement erronées. La stratégie va dépendre de la remise ou non dans le paquet des cartes tirées.

Ici les élèves voient assez vite que lorsque l’on lance deux dès la somme des deux faces est plus fréquemment 7. Pourtant la première explication qui vient à l’esprit lorsque l’on n’est pas familier de ce genre de problème laisserait supposer que les sommes 6, 7 et 8 sont équiprobables.

Quelques liens pour en savoir plus:
Fiche d’application pratique à lire pour bien comprendre comment utiliser les documents ci-dessous (me contacter)*
L’origine chinoise de la méthode

N’hésitez surtout pas à m’écrire à l’adresse :
desurtroy@gmail.com

Zhuangzi
L’auteur de cet article est professeur de classe exceptionnelle, ancien ingénieur, pratiquant d’arts martiaux, qui enseigne les mathématiques depuis 1994. Il a exercé pendant une quinzaine d’années en ZEP+, Zone de prévention violence, en région parisienne et en milieu pénitentiaire. Il a enseigné les mathématiques en Anglais sur l’Île Maurice puis à Londres, et dans un établissement chinois à Pékin.
Mesurer la hauteur d’une cheminée – 4èmes (Ile Maurice)
Sondage – 4èmes (Ile Maurice)
La Méthode des Cycles Chinois dans un établissement de Pékin
Recherche individuelle
Recherche en groupe