Introduction
un intervalle de confiance permet d’établir la marge d’erreur entre les données d’un sondage (échantillon) et les données de la population totale.
Les intervalles de confiance sont ainsi élaborés à partir d’un échantillon, extraite d’une population, notamment pour estimer des indicateurs statistiques comme la moyenne, la fréquence ou la variance.
Niveau de confiance
Il faut donc estimer un intervalle, correspondant à un niveau de confiance, dans laquelle la statistique recherchée à la plus grande probabilité de se trouver.
| Niveau de confiance α | Niveau de risque 1-α | Coefficient de confiance |
| 90% | 10% | 1,645 |
| 95% | 5% | 1,960 |
| 99% | 1% | 2,576 |
Les intervalles de confiance sont liés au niveau de confiance. Les niveaux de confiance sont exprimés en pourcentage (par exemple, un niveau de confiance de 90 %)
Pourquoi faire?
En statistique, les intervalles de confiance sont une méthode couramment utilisée pour indiquer la précision des valeurs estimées. Plus l’intervalle de confiance est élevé, moins les informations sont précises. Un intervalle de confiance inférieur est plus susceptible de renvoyer la valeur exacte.
Pour cette raison, l’écart type de la variance ou de l’intervalle de confiance est généralement spécifié en plus de la moyenne calculée.
Niveau de confiance à 95 % est le plus couramment choisi.
Intervalle de confiance : la formule
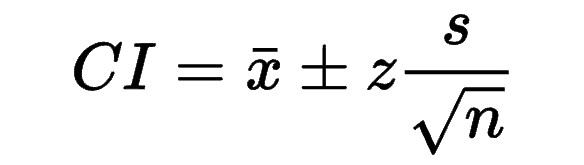
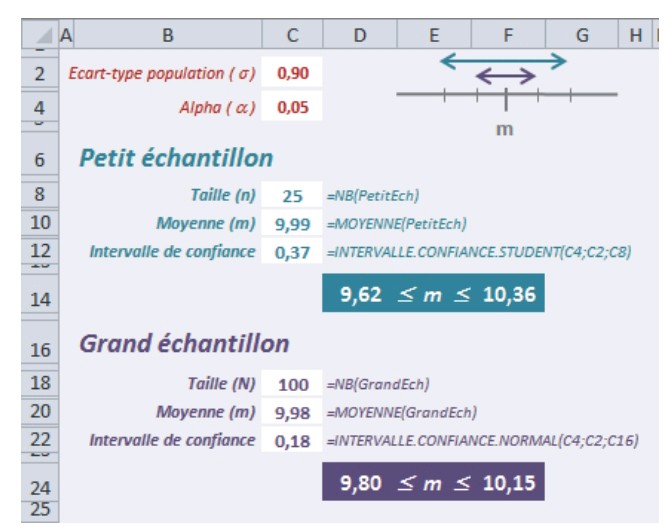
Intervalle de confiance : La fonction sur Excel
On utilisera la fonction suivante :
INTERVALLE.CONFIANCE.NORMALE(alpha ; écart-type ; taille)
avec
- alpha = Niveau de confiance utilisé pour calculer le niveau de confiance. Le niveau de confiance est égal à 100*(1 – alpha)%, ou en d’autres termes, un alpha de 0,05 indique un niveau de confiance de 95 %.
- Ecart-type = Représente l’écart-type de population pour la plage de données ; cet argument est supposé être connu.
- Taille = Représente la taille de l’échantillon (Effectif).
Cette fonction renvoie l’intervalle de confiance de la valeur attendue d’une variable aléatoire
Exemple :
=INTERVALLE.CONFIANCE.NORMALE(0,05; 2,5 ; 50) = 0,692951
On s’entraîne+
Exercice 1
Calculer l’intervalle de confiance au niveau de confiance 90%, 95% et 99% pour n = 120 ; μ = 35 et σ=15,08.
Exercice 2
Au guichet, un supporter attend pour acheter son billet. On modélise le temps d’attente en minute par une variable aléatoire X qui suit la loi normale d’espérance μ=30 et d’écart-type σ=10.
- En moyenne, combien de temps attend ce supporter au guichet ?
- Le supporter ne dispose que de 15 minutes avant le début du match pour acheter son billet. Quelle est la probabilité qu’il puisse acheter son billet avant le début du match ?
- Calculer l’intervalle de confiance de la moyenne au niveau de confiance 95%.
Exercice 3
Le service financier d’une grande chaîne de magasins désire estimer le montant moyen µ d’un achat dans le rayon sport à l’aide d’un sondage aléatoire. Un échantillon constitué de 90 achats a été prélevé dans un des magasins à Paris et à donner les résultats suivants
- moyenne µ d’un échantillon 33€
- écart-type de l’échantillon 6€
- Donner un intervalle de confiance de la moyenne au niveau 95%
- Quel taille d’échantillon faudrait-il envisager pour obtenir un intervalle de confiance de la moyenne au niveau de confiance 95% de largeur 1,6.
Exercice 4
Soit une population normale de moyenne µ inconnue et d’écart-type σ = 1,5. On y a prélevé un échantillon aléatoire simple d’effectif n = 9.
Les observations sont les suivantes :
24,3 ; 24,7 ; 23,2 ; 23,8 ; 24,5 ; 26 ; 25,4 ; 24,8 ; 23,8
trouver un intervalle de confiance pour µ au niveau de confiance de 95%.
Exercice 5
Des études statistiques ont permis de modéliser le temps hebdomadaire, en heures, de connexion à internet des jeunes en France âgés de 16 à 24 ans par une variable aléatoire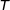 
suivant une loi normale de moyenne µ = 13,9 et d’écart-type 
.
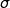La fonction densité de probabilité de T est représentée ci-dessous :
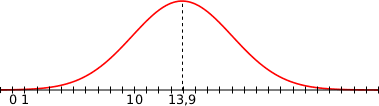
On sait que P(T >= 22) = 0,023
En exploitant cette information :
a) Hachurer sur le graphique, deux domaines distincts dont l’aire est égale à 0,023.
b) Déterminer P(5,8 < T < 22). Justifier le résultat.
c) À la demande de la Hadopy, un institut de sondage réalise une enquête sur un échantillon de taille 1500, il dénombre 625 réponses « Oui ».
Donner un intervalle de confiance, au niveau de confiance de 95 %, de la proportion q de jeunes qui répondent « Oui » à un tel sondage, parmi la population des jeunes français âgés de 16 à 24 ans.
Exercice 6
Sur un court de tennis, un lance-balle permet à un joueur de s’entraîner seul. Cet appareil envoie des balles une par une à une cadence régulière. Le joueur frappe alors la balle puis la balle suivante arrive.
Suivant le manuel du constructeur, le lance-balle envoie au hasard la balle à droite ou à gauche avec la même probabilité.
Le lance-balle est équipé d’un réservoir pouvant contenir 100 balles. Sur une séquence de 100 lancers, 42 balles ont été lancées à droite.
La proportion « théorique » de balles à droites est p = 0,5
Le joueur doute alors du bon fonctionnement de l’appareil. Ses doutes sont-ils justifiés ?
Pour répondre à cette question on peut utiliser un intervalle de fluctuation asymptotique à 95 %.
More Stories
TD N°4 Évaluation Tableaux Croisées Dynamiques et Prévisions Sur Excel
B2 – TD N°3 Tableaux Croisés Dynamiques TCD, Bases De Données BDD & Tableaux Excel
TD N°1 La Loi Normale • Table de Gauss • Calcul de Probabilités avec Excel • Variable Aléatoire