La dernière partie de mécanique du programme de bac 2013 concerne l’application des lois de Newton au mouvement des planètes et des satellites. Voyons les compétences à maîtriser.

Note : dans l’article qui suit, les vecteurs sont notés en gras. g est le vecteur gravitation tandis que g est la valeur de la gravitation. On peut écrire : g=9,8 N/kg mais on écrira g=-g.k où k est le vecteur unitaire vertical.

Je sais interpréter un mode de propulsion par réaction à l’aide d’un bilan qualitatif de quantité de mouvement.

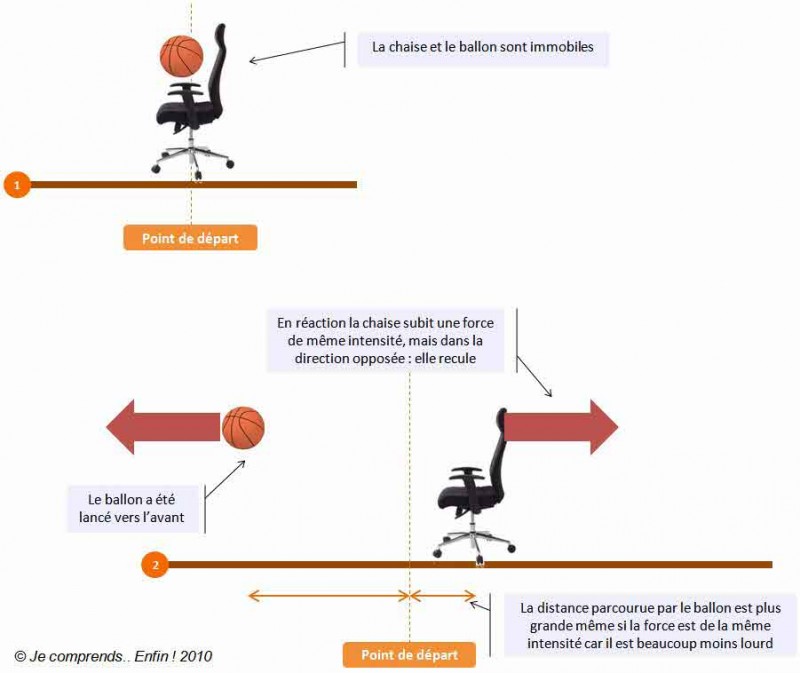
Il ne s’agit pas à proprement parler d’une application des lois de Newton au mouvement des planètes mais c’est une compétence qu’on risque de trouver dans un exercice sur la satellisation puisque c’est le mode de propulsion des fusées. Pour comprendre utilisons cette image issue du site je comprends enfin :

Dans cet exemple, le système constitué de la balle et de la chaise est pseudo-isolé, c’est à dire que les forces qui agissent sur le système se compensent. Ainsi, la seconde loi de Newton mène à dp/dt=0 et donc la quantité de mouvement totale se conserve.
Initialement, la quantité de mouvement est nulle, par conséquent, une fois que le ballon a quitté la chaise, la somme vectorielle des quantités de mouvement du ballon et de la chaise doit être nulle : p_ballon+p_chaise=0  soit p_ballon = –p_chaise ainsi, les valeurs des quantités de mouvement sont égales et p_ballon=p_chaise (attention, noter le passage aux normes des vecteurs qui fait disparaître le signe moins). La quantité de mouvement de la chaise, donc sa vitesse, augmente avec l’éjection du ballon. Ce raisonnement est identique pour les fusées.

Le programme stipule bien qu’il n’est pas exigible de bilan quantitatif mais nous pouvons néanmoins en ébaucher un pour comprendre pourquoi le ballon part vite alors que la chaise part doucement : exprimons la conservation de la quantité de mouvement m_ballon.v_ballon=m_chaise.v_chaise ainsi, v_chaise=(m_ballon/m_chaise).v_ballon et la vitesse de la chaise est proportionnelle au rapport de la masse du ballon à celle de la chaise. S’il y a un rapport 10 (ballon de 100 g, chaise de 1 kg, par exemple), la chaise aura une vitesse 10 fois moins élevée que celle du ballon.

Pour les fusées, c’est le même raisonnement : les gaz sont éjectés avec une vitesse de l’ordre de 3000 m/s à un débit de 3-4 tonne par seconde mais la fusée a une masse de l’ordre de 1000 tonnes, donc son gain de vitesse est de l’ordre de 10 m/s à chaque seconde. Initialement le décollage est très lent, puis au fur et à mesure qu’elle éjecte du gaz, elle devient de moins en moins lourde et le gain en vitesse à chaque seconde devient de plus en plus élevé ce qui lui permet d’atteindre la vitesse de satellisation.

Mais au fait quelle est cette vitesse de satellisation ? Voici les compétences exigibles qui permettent de les calculer :

Je sais démontrer que, dans l’approximation des trajectoires circulaires, le mouvement d’un satellite, d’une planète, est uniforme.

Prenons un satellite ou une planète P au voisinage, respectivement d’une planète ou d’un astre S.

P n’est soumis(e) qu’à l’attraction gravitationnelle exercée par S qui s’écrit

F_S/P=- G.M_S.M_P/d_SP².u_SP
où u_SP est le vecteur unitaire porté par SP, allant de S vers P.

Ainsi, la seconde loi de Newton s’écrit dans le référentiel centré sur S, considéré comme galiléen :

?f_ext=m.a ? – G.M_S.M_P/d_SP².u_SP = M_P.a_P ? – G.M_S/d_SP².u_SP = a_P

Cette équation un peu compliquée nous donne toutes les trajectoires possibles pour un corps soumis à l’attraction gravitationnelle d’un autre. Et il y en a beaucoup. Vous pouvez jouer avec grâce à la simulation proposée par l’université du colorado.
Fort heureusement pour vous, il est hors de question de tout comprendre à l’exploitation de cette équation. Il est juste demandé de savoir l’interpréter dans le cas d’un mouvement circulaire. Dans ces conditions, on écrit simplement que d_SP=R et l’équation devient :

a_P=- G.M_S/R².u_SP

Ainsi, l’accélération est centripète, toujours centrée sur le cercle de la trajectoire. Centripète, tiens, tiens, mais ça nous dit quelque chose ça, non ? Mais oui, bien sûr c’est ce que l’on a vu dans le cours sur le mouvement circulaire. Pour un mouvement circulaire, si l’accélération est centripète, le mouvement est uniforme. Ainsi, nous venons de démontrer que dans l’approximation des mouvements circulaires, le mouvement d’un satellite ou d’une planète est uniforme. Vous n’êtes pas convaincu ? Alors relisez tranquillement cette démonstration avec un crayon à la main pour refaire la démo, vous verrez, ça marche.

Je sais établir l’expression de la vitesse et de la période d’un satellite, d’une planète

Nous avons donc montré que si le mouvement d’une planète est circulaire, alors il est uniforme. Donc il a pour expression : a_P = – v²/R.u_SP .(voir le cours sur le mouvement circulaire). En identifiant cette expression avec celle obtenue précédemment, on peut écrire que  – G.M_S/R².u_SP = – v²/R.u_SP . En simplifiant un peu, j’obtiens :  G.M_S/R²= v²/R qui me permet d’obtenir l’expression de la vitesse : soit v=?(G.M_S/R) – se lit racine de G.M_S sur R.
Résumons-nous. Si l’on place un objet à une distance d_SP d’un astre ou d’une planète et qu’on le lance avec une vitesse v=?(G.M_S/ R) perpendiculaire à l’axe SP, alors il aura un mouvement circulaire uniforme.

Mais quel est le rapport avec la période de révolution du satellite ou de la planète ? D’abord de quoi s’agit-il ? La période de révolution d’une planète est la durée nécessaire pour que la planète fasse un tour complet autour de l’astre tandis que la période de rotation propre est la durée pour qu’elle fasse un tour sur elle-même. Attention, il ne faut pas confondre, ça n’est pas du tout la même chose : pour la terre, la période de révolution autour du soleil est environ de 365 jours alors que la période de rotation propre est de 24 h – cela veut dire que la terre fait 365 tours sur elle-même lorsqu’elle n’a fait qu’un tour autour du soleil.

En une période de révolution, l’objet (satellite ou planète) a fait un tour autour de son centre de rotation. Ainsi, il a parcouru 2?R en un temps T. Sa vitesse est donc v=2?R/T. Voici donc la relation liant la vitesse v, la période de révolution T et le rayon de la trajectoire dSP.
Voyons l’exploitation de cette relation :
on a vu que pour le mouvement circulaire uniforme, v=?(G.M_S/ R) ainsi, si l’on identifie les deux expressions, on obtient :

2?R/T = ?(G.M_S R )
soit T = 2? ?( R³ / GM_S)
oui oui, il faut bidouiller un peu pour arriver à cela

Ouf ! Nous y sommes arrivé : nous avons pu obtenir la période de révolution d’un objet en fonction de sa distance à son astre attracteur.
Pour une planète, l’exploitation de cette relation nous donne quelque chose comme 365 jours pour une masse égale à celle du soleil et une distance égale à celle de la terre. Normal.
Cette expression est intéressante à exploiter dans le cas des satellites. Ainsi, en prenant pour Ms, les  5,98.10²⁴ kg de masse de la terre et R l’orbite moyenne de la navette ou de la station spatial internationale, c’est à dire 400 km, on obtient T=5600 s soit environ 1 h30. Et oui, en orbite à 400 km, on fait un tour de terre en 1h 30 !

Je connais les trois lois de Képler

Les lois de Képler (d’après Johannes Képler, 1571 – 1630) s’énoncent comme suit :
1. Les planètes du système solaire décrivent des trajectoires elliptiques dont le Soleil occupe l’un des foyers.
Rappelons qu’une ellipse est caractérisée par ces foyers S et S’ tels que SP+S’P=2a où a est le demi grand axe :

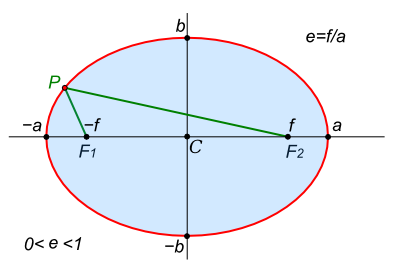
Le rapport entre le demi-grand axe a et f, la distance entre le foyer et le centre de symétrie de l’ellipse est l’excentricité e=f/a. Si e=0 alors l’ellipse est un cercle. Dans le système solaire, les planètes décrivent des ellipses très proches du cercle. Pour la terre, par exemple, e=0,017.
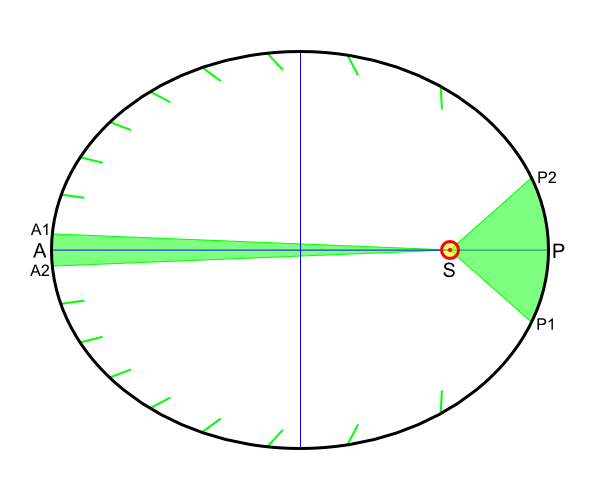
2. Le segment Soleil-Planète balaie des aires égales au cours de durées égales.
Ceci implique que les planètes et les comètes accélèrent lorsqu’elles se rapprochent du soleil :

En effet, afin d’assurer l’égalité des aires A1SA2 et P1SP2 balayées par la planète pendant une même durée, il est nécessaire que la planète parcourt P1P2 plus rapidement que  A1A2.
3. Le rapport T²/a³ a la même valeur pour toutes les planètes, cette valeur ne dépendant que de l’astre attracteur. T est la période de révolution et a, le demi-grand axe de la trajectoire balayée par la planète.
Nous avons vu en utilisant les lois de Newton que cette valeur constante est égale à 4?²/GMS. Ainsi, l’observation du mouvement des planètes du système solaire permet de déterminer la masse du soleil.
Bien que Képler les ait déterminées à partir du mouvement des planètes du système solaire, ces lois sont valables pour tout système centré comme une planète et ses satellites ou n’importe quel autre système planétaire.

Je sais exploiter la troisième loi de Kepler dans le cas d’un mouvement circulaire.

Par exemple, la lune est située à 380 000 km et sa période de révolution est de 27,3 jours. Sachant que T² / d³_SP  = 4?² / G.M_S on en déduit que M_S= (4?² / G).(d³_SP /T²) soit 6,0 x 10²⁴ kg.

Une application de tout cela :

[dailymotion]http://www.dailymotion.com/video/xx4a9c_satellites-espions_school[/dailymotion]
Vidéo extraite de delaphysique.com sur les satellites espions