La séquence « COMPRENDRE : temps, mouvement et évolution » du programme de TS 2012 – bac 2013 commence par la cinématique et la dynamique Newtonnienne. Il y a une dizaine de compétences exigibles dans cette partie qui sont plus ou moins longues et complexes à acquérir. Commençons par la cinématique et les lois de la dynamique.
Note : dans l’article qui suit, les vecteurs sont notés en gras.
Voici ce que le programme exige que vous sachiez sur cette partie :
Je sais extraire et exploiter des informations relatives à la mesure du temps pour justifier l’évolution de la définition de la seconde.
Difficile de se préparer à une telle compétence. On pourra, pour se mettre les idées en place, lire l’article de wikipedia sur la seconde.
A l’époque où l’on mesurait le temps avec la course du soleil, la seconde était définie comme une fraction du jour solaire.
Puis vint le temps où l’on prit en compte le fait que cette rotation évolue au cours des siècles et où l’on décida que la seconde serait définie comme une fraction de la durée que met la terre pour faire un tour complet autour du soleil, c’est à dire une fraction de l’année.
Maintenant, pour plus de précision et d’universalité, la seconde n’est plus définie à partir du mouvement de la terre mais à partir de la période de l’onde émise par un atome de Césium lorsqu’un de ses électrons passe d’une couche électronique à l’autre.
[dailymotion]http://www.dailymotion.com/video/xx49c9_la-mesure-du-temps_school#.UQ1GPpHkD1g[/dailymotion]
Vidéo extraite de delaphysique.com qui revient sur la mesure du temps
Je sais choisir un référentiel d’étude.
Les principaux référentiels d’étude utilisés en terminale sont :
- Référentiel terrestre : celui de la vie de tous les jours. Pour étudier le mouvement des objets de notre environnement quotidien et du laboratoire.
- Référentiel géocentrique : celui centré sur la terre dans laquelle celle-ci a un mouvement de rotation sur elle-même. C’est à dire qu’il est tel que les étoiles lointaines y sont fixes. Pour étudier le mouvement des satellites naturel (la lune) et artificiels.
- Référentiel héliocentrique : référentiel centré sur le soleil dans lequel les étoiles lointaines sont fixes. Pour étudier le mouvement des planètes.
- Référentiel jovien : le référentiel utilisé pour étudier le mouvement des satellites de Jupiter. Analogue au référentiel géocentrique mais pour Jupiter.
Je sais reconnaître des mouvements (rectiligne uniforme, rectiligne uniformément varié, circulaire uniforme, circulaire non uniforme) et donner dans chaque cas les caractéristiques du vecteur accélération.
Reconnaître des mouvements n’est pas bien compliqué. Donner les caractéristiques du vecteur accélération est une autre paire de manche. Tout d’abord, il faut bien comprendre ce qu’est le vecteur accélération : c’est le taux de variation du vecteur vitesse : a=?v/?t
 Pour bien définir le vecteur accélération, il faut avoir une idée claire sur ce qu’on appelle la vitesse. Dans la vie de tous les jours, la vitesse est un scalaire (un chiffre), alors qu’en physique c’est un vecteur, défini par sa norme, sa direction et son sens. Sa norme correspond à la définition de la vie de tous les jours : la distance parcourue par unité de temps (la seconde en physique), sa direction est tangente à la trajectoire et son sens est celui du mouvement.
Pour bien définir le vecteur accélération, il faut avoir une idée claire sur ce qu’on appelle la vitesse. Dans la vie de tous les jours, la vitesse est un scalaire (un chiffre), alors qu’en physique c’est un vecteur, défini par sa norme, sa direction et son sens. Sa norme correspond à la définition de la vie de tous les jours : la distance parcourue par unité de temps (la seconde en physique), sa direction est tangente à la trajectoire et son sens est celui du mouvement.
Mouvement rectiligne uniforme : la trajectoire est une droite, la vitesse est constante, l’accélération est nulle.
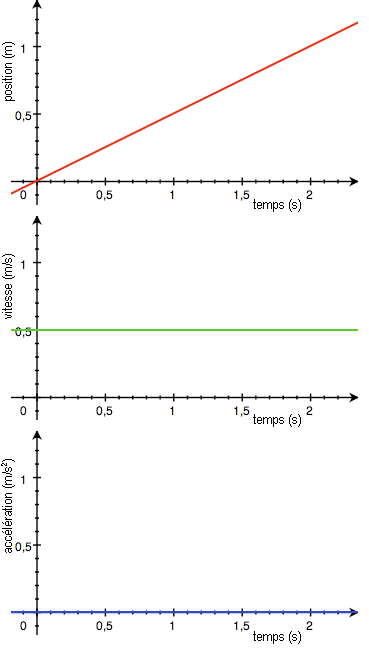
Mouvement rectiligne uniformément varié : la trajectoire est une droite, la vitesse est une proportionnelle au temps, le vecteur accélération est constant.
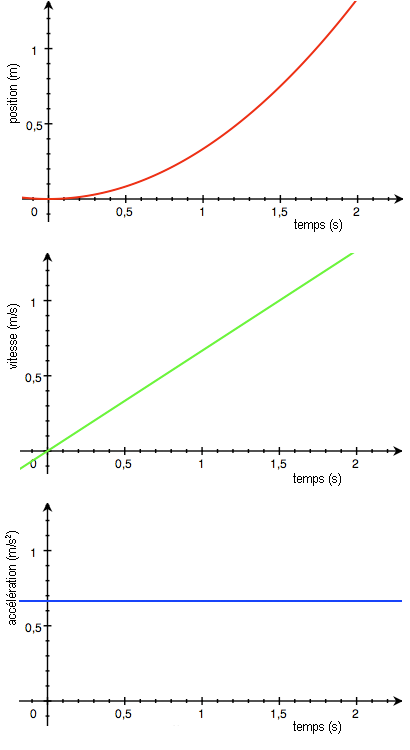
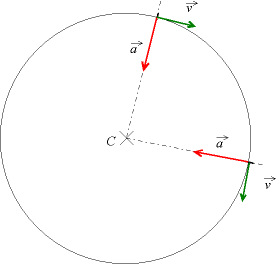
Mouvement circulaire uniforme: la trajectoire est un cercle, la vitesse est constante. Pour autant le vecteur vitesse varie a chaque instant. Par conséquent le vecteur accélération est non nul : centripète (dirigé vers le centre du cercle), il change sans cesse de direction. Sa valeur est par contre constante et égale à v²/R.
Mouvement circulaire non uniforme: la trajectoire est toujours un cercle mais la vitesse varie. Le vecteur accélération admet cette fois-ci deux composantes : l’une tangentielle au mouvement et égale à la dérive de v par rapport au temps et l’autre, normale au mouvement (comme dans le cas circulaire uniforme) dont la valeur est constante et égale à v²/R.
Je sais définir la quantité de mouvement p d’un point matériel.
Le vecteur quantité de mouvement p est égal au produit de la masse par la vitesse : p=m.v
Nous en aurons besoin pour la suite :
Je connais les trois lois de Newton
Première loi : également appelée principe d’inertie
Dans un référentiel galiléen, si le vecteur vitesse vG du centre d’inertie G du solide ne varie pas, la somme des forces extérieures qui s’exercent sur le solide est nulle et réciproquement : 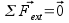
Cette loi est généralement appliquée aux solides au repos ou en mouvement de translation rectiligne uniforme pour déterminer les forces qui s’y appliquent (par exemple pour un palet qui glisse sans frottement, la réaction de la glace est exactement opposée au poids du palet).
Seconde loi : également appelé Postulat Fondamental de la Dynamique (PFD)
Dans un référentiel galiléen, la somme des forces extérieures appliquées à un solide est égale à la dérivée par rapport au temps de son vecteur quantité de mouvement : ![]() .
.
Dans le cas où la masse est constante, cette seconde loi devient : 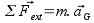
Dans cette dernière expression, les forces s’expriment en Newton (N), la masse en kilogramme (kg) et l’accélération en mètre par seconde carré (m.s-2). Nous allons beaucoup l’utiliser par la suite pour déterminer les trajectoires d’objets en mouvement.
Troisième loi : également appelé le principe des actions réciproques
Si 2 corps sont en interaction, alors la force exercée par le premier sur le second est égale et opposée à la force exercée par le second sur le premier : 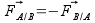
Cette loi s’oublie facilement et pourtant elle est fondamentale pour comprendre tout ce qui concerne la propulsion.
[Edit décembre 2013] : Toutes les explications en vidéo

4 thoughts on “Cinématique et dynamique Newtonnienne pour le bac 2013”