Objectif
Découvrir l’homothétie en deux séances
ÉNONCÉ

Niveau
Fin de cycle 4, 3ème
Pré-requis
- Avoir déjà utilisé GeoGebra
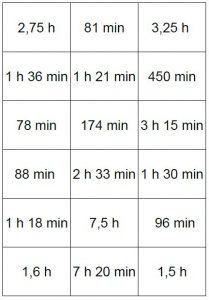
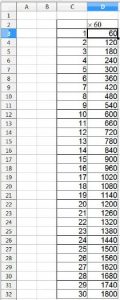
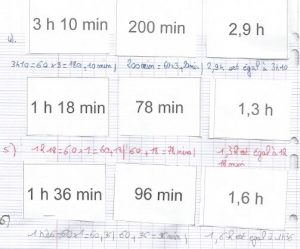
- Avoir déjà étudié un même type de tâche (inscrire une figure dans une autre), par exemple :
- De même, avoir déjà travaillé une question d’agrandissement, par exemple :


Déroulement
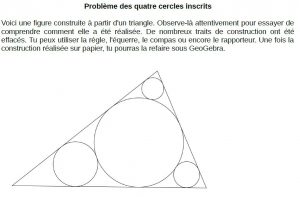
Commencer par montrer une figure dynamique sous GeoGebra afin de faire comprendre à la classe qu’il ne s’agit pas de reproduire une figure (statique) particulière mais que la construction doit pouvoir fonctionner sur tous les triangles possibles.
Dire aux élèves qu’ils vont devoir comprendre comment est construit le carré inscrit dans le triangle et qu’une fois la construction établie, ils pourront la réaliser sous GeoGebra.
Distribuer l’énoncé et mettre les élèves au travail : papier/crayon. Cette étape est importante, les élèves doivent prendre conscience de la difficulté de la construction. Comment faire en sorte que deux sommets soient sur deux côtés du triangle et que les deux autres sommets soient sur le même troisième côté ? On pourra distribuer des « figures pour comprendre ». Ce sont des figures déjà réalisées sur lesquelles les élèves peuvent effectuer des tracés, repérer des alignements, mesurer, bref explorer.
Relances / difficultés
Les élèves vont produire des figures qu’ils ont réalisés à tâtons. En montrer une à la classe via un vidéoprojecteur. Elle pourra sembler justes à certains et une discussion de classe permettra de l’invalider après en avoir aussi montré les aspects positifs. Il faudra alors relancer la classe pour la faire sortir de cette situation de blocage.
Une relance importante consiste à abaisser une contrainte :
| Construire un carré avec un sommet intérieur au triangle | Construire un carré avec un côté parallèle à un côté du triangle |
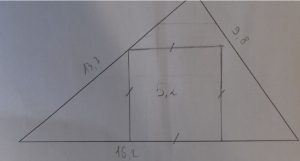 |
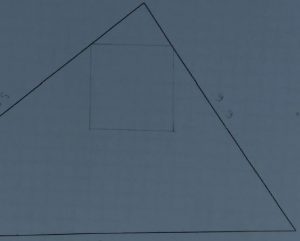 |
Une fois la contrainte abaissée, la figure est relativement simple à construire. Questionner alors les élèves sur la taille du carré ainsi construit. Le carré solution est un agrandissement du « petit » carré, comment le construire ? Peut-on construire des carrés de plus en plus grand ? Le carré pouvant même dépasser le carré solution. Une fois plusieurs carrés construits, peut-on trouver des alignements (sommets des carrés) ? Ces relances ont pour but d’obtenir des carrés homothétiques afin d’obtenir un sommet du carré solution :
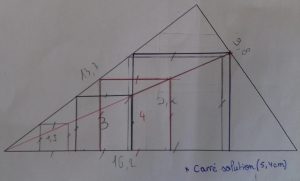 |
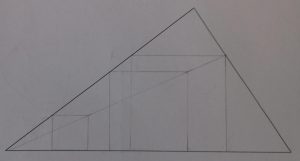 |
Une fois la construction réalisée par tous, lors d’une deuxième séance, passer sous GeoGebra. On pourra limiter les outils avec une version de GeoGebra « allégée » :
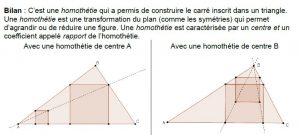
Institutionnalisation
Voici un bilan possible qui montre les aspects dynamiques de l’homothétie qui devient un outil pour construire.
Prolongements
- Lors de la séance sous GeoGebra, vérifier que la construction fonctionne dans tous les cas (lorsqu’un des angles de la « base » est obtus). Si ce n’est pas le cas demander de corriger, il faudra alors considérer les droites qui supportent les côtés du triangle et non pas seulement les segments.
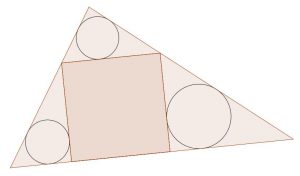
- Proposer de construire des carrés inscrits à l’infini (dans les trois triangles restants) ou de construire les trois cercles inscrits dans les trois triangles restants (Sangaku) :
 Conclusion
Conclusion
Il restera à faire le lien avec le théorème de Thalès, en effet, cette tâche ne prend pas en compte le rapport de l’homothétie.