- Les modalités et la date d’émergence de la bipédie restent âprement débattues, en particulier du fait d’un faible nombre de fossiles humains très anciens.
- Sahelanthropus tchadensis, découvert en 2001 au Tchad, est considéré comme le plus ancien représentant de l’humanité. La forme de son crâne suggère une station bipède.
- La description de trois os des membres de Sahelanthropus confirme une bipédie habituelle, mais pas exclusive.
- voir la suite ici
Archives de catégorie : Au fil de l’eau:dernières dépêches scientifiques!!!
Pourquoi la glace de mer en Antarctique résiste au réchauffement
Les modèles qui simulent les tourbillons océaniques au large de l’Antarctique permettent de comprendre l’étonnante stabilité de la glace de mer de l’océan austral face au changement climatique…voir la suite ici
Quand les variations de l’orbite terrestre dictent l’évolution biologique
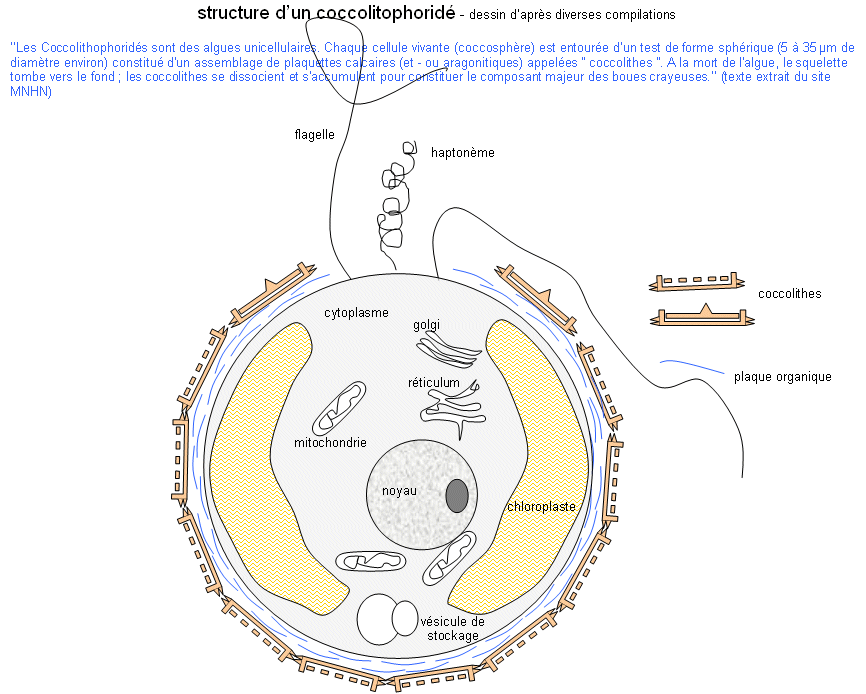
Les coccolithophores sont des micro-algues dont la particularité est de former autour de leur unique cellule de minuscules plaques de calcaire, les coccolithes, dont les formes varient selon les espèces.
Après leur mort, ces coccolithes sédimentent dans les fonds marins qui ont fidèlement archivé les détails de l’évolution de ces organismes. Une équipe menée par des scientifiques du CNRS1 montre dans Nature le 1er décembre 2021 que certaines variations de l’orbite terrestre ont influé sur l’évolution de ces micro-algues. Pour cela, pas moins de 9 millions de coccolithes, couvrant une période de 2,8 millions d’années et plusieurs localisations dans l’océan tropical, ont été étudiés par microscopie automatisée et classés par espèce en utilisant l’intelligence artificielle. Les scientifiques observent que les coccolithophores ont connu des cycles de diversification et d’uniformisation, avec des rythmes de 100 et 400 milliers d’années. Ils en trouvent aussi la cause : la forme plus ou moins aplatie de l’orbite de la Terre autour du Soleil, variant au même rythme…voir la suite ici
Alain Gallien source SVT Ac Dijon
Quand l’eau devient métallique
En faisant réagir de l’eau avec des métaux alcalins, il est possible de modifier ses propriétés pour la transformer en un métal conducteur.
Les reflets dorés de cette goutte d’eau sont un signe qu’elle est devenue… métallique?! Explications. On sait que la plupart des matériaux isolants peuvent devenir conducteurs lorsqu’ils sont soumis à de fortes pressions. Dans ces conditions, les atomes et les molécules sont comprimés à un point tel que leurs électrons deviennent libres de circuler dans le matériau et donc de conduire un courant électrique, comme dans un métal. Il en serait ainsi de l’hydrogène dans les profondeurs des planètes géantes Jupiter et Saturne, et de l’eau dans les couches internes de Neptune et Uranus. Pourtant, l’eau pure est un très mauvais conducteur. Dans la vie quotidienne, c’est la présence d’ions dans l’eau qui la rend conductrice. Pour transformer de l’eau pure en métal, il faudrait exercer une pression de 15 millions de bars (1 bar correspond environ à la pression de l’atmosphère terrestre). Philip Mason, de l’Académie des sciences tchèque, à Prague, et ses collègues ont trouvé une autre solution pour réaliser cette  transformation… voir la suite sur Pour la Science
transformation… voir la suite sur Pour la Science